2023-2024學年江蘇省南通市海安高級中學高二（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合M，N滿足M∩N≠?，則（　　）

  A．?x∈M，x∈N

  B．?x∈M，x?N

  C．?x∈M，x∈N

  D．?x∈M，x?N
  組卷：72引用：6難度：0.8

  解析

• 2．復數

  1

  +

  i

  i

  3

  （i是虛數單位）在復平面上對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：65引用：7難度：0.9

  解析

• 3．設m為實數，已知直線l₁：2x+3y-2=0，l₂：mx+（2m-1）y+1=0，若l₁∥l₂，則m的值為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：167引用：2難度：0.9

  解析

• 4．“-1＜m＜3”是“方程

  x

  2

  m

  +

  1

  +

  y

  2

  7

  -

  m

  =1表示橢圓”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：228引用：10難度：0.7

  解析

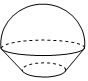• 5．某校科技社利用3D打印技術制作實心模型．如圖，該模型的上部分是半球，下部分是圓臺．其中半球的體積為144πcm³，圓臺的上底面半徑及高均是下底面半徑的一半．打印所用原料密度為1.5g/cm³，不考慮打印損耗，制作該模型所需原料的質量約為（1.5π≈4.7）（　　）

  A．3045.6g

  B．1565.1g

  C．972.9g

  D．296.1g
  組卷：190引用：3難度：0.5

  解析

• 6．已知函數

  f

  （

  x

  ）

  =

  sinxcosx

  -

  3

  co

  s

  2

  x

  +

  3

  2

  ，則下列說法正確的是（　　）

  A． f （ x ） = sin （ 2 x - π 3 ）

  B．函數f（x）的最小正周期為π

  C．函數f（x）的對稱軸方程為 x = kπ + 5 π 12 （ k ∈ Z ）

  D．函數f（x）的圖象可由y=sin2x的圖象向右平移 π 6 個單位長度得到
  組卷：206引用：4難度：0.8

  解析

• 7．已知在各項為正的等比數列{a_n}中，a₂與a₈的等比中項為8，則4a₃+a₇取最小值時首項a₁ 等于（　　）

  A．8

  B．4

  C．2

  D．1
  組卷：97引用：6難度：0.7

  解析

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟．

• 21．如圖，已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）上一點A（0，

  2

  ），右焦點為F（c,0），直線AF交橢圓于B點，且滿足|AF|=2|FB|，|AB|=

  3

  3

  2

  ．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）若直線y=kx（k＞0）與橢圓相交于C，D兩點，求四邊形ACBD面積的最大值．
  組卷：202引用：3難度：0.3

  解析

• 22．對于橢圓：

  y

  2

  a

  2

  +

  x

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  ，我們稱雙曲線：

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =

  1

  為其伴隨雙曲線．已知橢圓C：

  y

  2

  3

  +

  x

  2

  b

  2

  =

  1

  （

  0

  ＜

  b

  ＜

  3

  ），它的離心率是其伴隨雙曲線Γ離心率的

  2

  2

  倍．
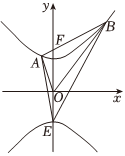
  （1）求橢圓C伴隨雙曲線Γ的方程；
  （2）如圖，點E，F分別為Γ的下頂點和上焦點，過F的直線l與Γ上支交于A，B兩點，設△ABO的面積為S，∠AOB=θ（其中O為坐標原點）．若△ABE的面積為

  6

  +

  3

  3

  ，求

  S

  tanθ

  ．
  組卷：158引用：8難度：0.4

  解析