2022年內蒙古包頭市青山區北重二中中考數學三模試卷

一．選擇題

• 1．

  16

  的算術平方根是（　　）

  A．2

  B．4

  C．±2

  D．±4
  組卷：5724引用：27難度：0.9

  解析

• 2．北京作為全球首個雙奧之城，于2月4日至2月20日舉辦第24屆冬奧會，本屆冬奧會匯聚了世界各國的運動員，伴隨著中國以及數字媒體的發展，北京冬奧會創造了多項記錄：數字化互動最廣泛的冬奧會、轉播時長最長的冬奧會以及開幕式收視率最高的冬奧會，在賽事期間，創紀錄的6400多萬人使用奧林匹克網站和App關注冬奧會，數字6400用科學記數法可表示為（　　）

  A．6.4×103

  B．64×102

  C．6.4×107

  D．6.4×108
  組卷：40引用：1難度：0.9

  解析

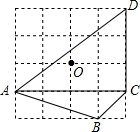• 3．如圖為4×4的網格圖，A，B，C，D，O均在格點上，點O是（　　）

  A．△ACD的外心

  B．△ABC的內心

  C．△ACD的內心

  D．△ABC的外心
  組卷：3671引用：34難度：0.7

  解析

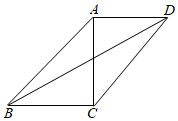• 4．如圖，在四邊形ABCD中，∠ACB=∠CAD=90°，AC=CB，sin∠ACD=

  3

  5

  ，則tan∠BDC的值是（　　）

  A． 3 3

  B． 3 6

  C． 16 37

  D． 16 25
  組卷：826引用：3難度：0.5

  解析

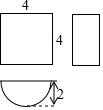• 5．一個幾何體的三視圖如圖所示，則該幾何體的表面積是（　　）

  A．24+2π

  B．16+4π

  C．16+8π

  D．16+12π
  組卷：1116引用：9難度：0.7

  解析

• 6．在六張卡片上分別寫有

  8

  ，

  22

  7

  ，0，π，-6，

  4

  六個數，從中任意抽取一張，卡片上的數為無理數的概率是（　　）

  A． 1 6

  B． 1 3

  C． 1 2

  D． 2 3
  組卷：104引用：2難度：0.6

  解析

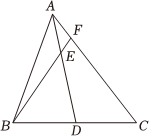• 7．AD是△ABC的中線，E是AD上一點，AE=

  1

  4

  AD，BE的延長線交AC于F，則

  AF

  AC

  的值為（　　）

  A． 1 4

  B． 1 5

  C． 1 6

  D． 1 7
  組卷：3941引用：16難度：0.7

  解析

• 8．以下四個命題中真命題是（　　）
  ①若a²=b²，則a=b；
  ②順次連接四邊形各邊中點所得的四邊形一定是平行四邊形；
  ③方程x²-x-1=0有兩個不相等的實數根；
  ④六邊形的內角和是外角和的2倍．

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：75引用：2難度：0.6

  解析

三．解答題

• 24．已知正方形ABCD，E，F為平面內兩點．
  
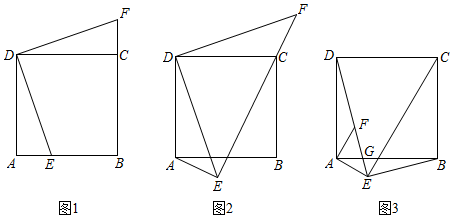
  【探究建模】
  （1）如圖1，當點E在邊AB上時，DE⊥DF，且B，C，F三點共線．求證：AE=CF；
  【類比應用】
  （2）如圖2，當點E在正方形ABCD外部時，DE⊥DF，AE⊥EF，且E，C，F三點共線．猜想并證明線段AE，CE，DE之間的數量關系；
  【拓展遷移】
  （3）如圖3，當點E在正方形ABCD外部時，AE⊥EC，AE⊥AF，DE⊥BE，且D，F，E三點共線，DE與AB交于G點．若DF=3，AE=

  2

  ，求CE的長．
  組卷：2498引用：17難度：0.1

  解析

• 25．如圖，在平面直角坐標系中，直線y=

  1

  2

  x+2與x軸交于點A，與y軸交于點C，拋物線y=-

  1

  2

  x

  2

  +bx+c經過A、C兩點，與x軸的另一交點為點B．
  （1）求拋物線的函數表達式；
  （2）連接BC、CD，設直線BD交線段AC于點E，求

  DE

  EB

  的最大值；
  （3）過點D作DF⊥AC，垂足為點F，連接CD，是否存在點D，使得△CDF中的∠DCF=2∠BAC，若存在，求出點D的坐標；若不存在，請說明理由．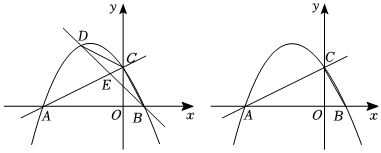
  
  組卷：307引用：1難度：0.1

  解析