2021-2022學(xué)年天津市西青區(qū)楊柳青一中高二（下）期末數(shù)學(xué)試卷

一、選擇題：本題共9小題，每小題5分，共45分。在每小題給出的四個選項中只有一項是符合題目要求的，請將正確答案的序號填涂到答題卡上。

• 1．集合U={-2，-1，0，1，2，3}，A={-1，0，2，3}，B={-1，1，3}，則A∩（?_UB）=（　　）

  A．{-1，1，3}

  B．{0，2}

  C．{-1，0，2}

  D．{0，1，2}
  組卷：209引用：1難度：0.7

  解析

• 2．已知x∈R，則“|x-1|＜2”是“（x+1）（x-5）≤0”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：560引用：1難度：0.7

  解析

• 3．函數(shù)

  f

  （

  x

  ）

  =

  2

  x

  -

  1

  （

  x

  -

  1

  ）

  2

  的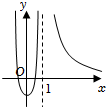大致圖象是（　　）

  A．

  B．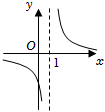

  C．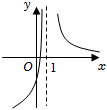

  D．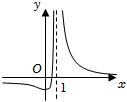
  組卷：166引用：2難度：0.9

  解析

• 4．兩個具有線性相關(guān)關(guān)系的變量的一組數(shù)據(jù)（x₁，y₁），（x₂，y₂），…，（x_n，y_n），下列說法錯誤的是（　　）

  A．相關(guān)系數(shù)越接近1，變量x,y相關(guān)性越強

  B．落在回歸直線方程上的樣本點越多，回歸直線方程擬合效果越好

  C．相關(guān)指數(shù)R2越小，殘差平方和越大，即模型的擬合效果越差

  D．若x表示女大學(xué)生的身高，y表示體重，則R2≈0.64表示女大學(xué)生的身高解釋了64%的體重變化
  組卷：157引用：1難度：0.8

  解析

• 5．若ln2=a,ln3=b,則log₈18=（　　）

  A． a + 3 b a 3

  B． a + 2 b 3 a

  C． a + 2 b a 3

  D． a + 3 b 3 a
  組卷：819引用：1難度：0.8

  解析

• 6．設(shè)a=log₃2，b=ln3，

  c

  =

  5

  -

  1

  2

  ，則a,b,c的大小關(guān)系為（　　）

  A．c＜a＜b

  B．a(chǎn)＜c＜b

  C．b＜a＜c

  D．c＜b＜a
  組卷：246引用：3難度：0.7

  解析

• 7．已知拋物線y²=2px（p＞0）上一點M（1，m）到其焦點的距離為5，雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左頂點為A且離心率為

  5

  2

  ，若雙曲線的一條漸近線與直線AM垂直，則雙曲線的方程為（　　）

  A． x 2 - y 2 4 = 1

  B． x 2 4 - y 2 = 1

  C．x2-2y2=1

  D．x2-4y2=1
  組卷：1057引用：7難度：0.7

  解析

三、解答題：本大題共5小題，共75分。解答應(yīng)寫出文字說明，證明過程或演算步驟.

• 20．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的焦距為

  2

  3

  ，且經(jīng)過點A（0，-1），過點A的直線l與橢圓交于點B．
  （Ⅰ）求橢圓C的標(biāo)準(zhǔn)方程；
  （Ⅱ）設(shè)M為線段AB的中點，O為原點，OM所在的直線與橢圓C交于P，Q兩點（點Q在x軸上方），問是否存在直線l使得△AMQ的面積是△BMO面積的6倍？若存在，求直線l的方程，并求此時四邊形APBQ的面積，若不存在，請說明理由．
  組卷：246引用：2難度：0.5

  解析

• 21．已知函數(shù)f（x）=e^x-1-x-ax²．
  （Ⅰ）當(dāng)a=0時，
  （ⅰ）求f（x）在點（1，f（1））處的切線方程；
  （ⅱ）求f（x）的最小值；
  （Ⅱ）當(dāng)x≥0時，若不等式f（x）≥0恒成立，求實數(shù)a的取值范圍；
  （Ⅲ）當(dāng)x＞0時，證明（e^x-1）ln（x+1）＞x²．
  組卷：391引用：4難度：0.3

  解析