2022-2023學(xué)年江蘇省南京市浦口區(qū)江浦高級中學(xué)高一（上）段考數(shù)學(xué)試卷（12月份）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知角α=2023°，則α的終邊在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：747引用：6難度：0.8

  解析

• 2．函數(shù)f（x）=

  3

  x

  -

  2

  +

  1

  x

  -

  1

  的定義域為（　　）

  A．{x|x＞ 2 3 且x≠1}

  B．{x|x＜ 2 3 或x＞1}

  C．{x| 2 3 ≤x≤1}

  D．{x|x≥ 2 3 且x≠1}
  組卷：100引用：8難度：0.7

  解析

• 3．命題“?x≥1，都有2^x-1≥1”的否定是（　　）

  A．?x≥1，使得2x-1＜1	B．?x≥1，使得2x-1≥1
  C．?x≥1，都有2x-1＜1	D．?x＜1，使得2x-1＜1
  組卷：12引用：3難度：0.9

  解析

• 4．若

  a

  =

  （

  2

  5

  ）

  0

  .

  1

  ，

  b

  =

  （

  2

  5

  ）

  0

  .

  2

  ，

  c

  =

  lo

  g

  2

  5

  2

  ，則a,b,c的大小關(guān)系為（　　）

  A．a(chǎn)＜b＜c

  B．c＜b＜a

  C．c＜a＜b

  D．a(chǎn)＜c＜b
  組卷：151引用：4難度：0.7

  解析

• 5．函數(shù)y=

  -

  4

  |

  x

  |

  x

  2

  +

  1

  的圖象大致為（　　）

  A．

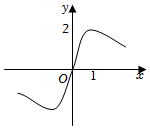
  B．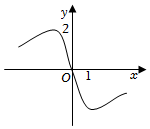

  C．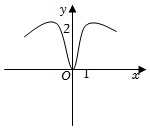

  D．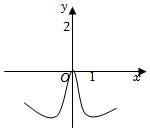
  組卷：178引用：4難度：0.7

  解析

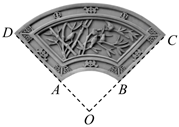• 6．磚雕是我國古建筑雕刻中的重要藝術(shù)形式，傳統(tǒng)磚雕精致細(xì)膩、氣韻生動、極富書卷氣．如圖所示，一扇環(huán)形磚雕，可視為將扇形OCD截去同心扇形OAB所得圖形，已知OA=0.2m,AD=0.3m,∠AOB=100°，則該扇環(huán)形磚雕的面積為（　　）m²．

  A． π 6

  B． π 12

  C． π 18

  D． 7 π 120
  組卷：253引用：9難度：0.7

  解析

• 7．已知正數(shù)x,y滿足x+4y-xy=0，則

  4

  x

  +

  y

  的最大值為（　　）

  A． 1 3

  B． 4 9

  C． 3 7

  D．1
  組卷：678引用：5難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

• 21．已知產(chǎn)品利潤等于銷售收入減去生產(chǎn)成本．若某商品的生產(chǎn)成本C（單位：萬元）與生產(chǎn)量x（單位：千件）間的函數(shù)關(guān)系是C=3+x；銷售收入S（單位：萬元）與生產(chǎn)量x間的函數(shù)關(guān)系是S=

  3 x + 18 x - 8 + 5 ， 0 ＜ x ＜ 6

  14 ， x ≥ 6

  ．
  （Ⅰ）把商品的利潤表示為生產(chǎn)量x的函數(shù)；
  （Ⅱ）當(dāng)該商品生產(chǎn)量x（千件）定為多少時獲得的利潤最大，最大利潤為多少萬元？
  組卷：222引用：9難度：0.5

  解析

• 22．已知定義在（-1，1）上函數(shù)f（x）滿足：當(dāng)x＞0時，f（x）＞0，且對?x,y∈（-1，1）都有f（x）+f（y）=f（x+y）?[1-f（x）?f（y）]．
  （1）求f（0）并寫出f（x）的奇偶性（直接寫，不要過程）；
  （2）判斷f（x）在區(qū)間（0，1）上的單調(diào)性并證明；
  （3）已知

  f

  （

  -

  1

  2

  ）

  =

  tan

  3

  π

  4

  ，g（x）=4^x-a?2^x，若

  ?

  x

  1

  ∈

  [

  -

  1

  2

  ，

  1

  2

  ]

  ，對?x₂∈[-1，1]，總有f（x₁）=g（x₂）成立，求a的取值范圍．
  組卷：49引用：2難度：0.4

  解析