2022-2023學(xué)年江西省撫州市黎川二中高二（下）期末數(shù)學(xué)試卷

一、單選題（每題5分，共40分）

• 1．在等差數(shù)列{a_n}中，若a₂+a₉=10，則3a₄+a₁₀=（　　）

  A．10

  B．15

  C．20

  D．25
  組卷：974引用：4難度：0.6

  解析

• 2．已知函數(shù)f（x）=

  x

  e

  x

  和g（x）=

  lnx

  x

  +b有相同的極大值，則b=（　　）

  A．0

  B．2

  C．-1

  D．-3
  組卷：196引用：4難度：0.5

  解析

• 3．已知數(shù)列{a_n}滿足a₂=

  1

  4

  ，且a_n+1=

  2

  a

  n

  -

  1

  2

  a

  n

  ，則a₂₀₂₃=（　　）

  A． 1 4

  B．-1

  C． 3 2

  D． 2 3
  組卷：76引用：3難度：0.8

  解析

• 4．設(shè)f（x）=sinx+cosx,那么（　　）

  A．f′（x）=cosx-sinx	B．f′（x）=cosx+sinx
  C．f′（x）=-cosx+sinx	D．f′（x）=-cosx-sinx
  組卷：184引用：10難度：0.9

  解析

• 5．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的離心率為

  5

  ，C的一條漸近線與圓（x-2）²+（y-3）²=1交于A，B兩點(diǎn)，則|AB|=（　　）

  A． 5 5

  B． 2 5 5

  C． 3 5 5

  D． 4 5 5
  組卷：3101引用：12難度：0.5

  解析

• 6．為了更好地解決就業(yè)問題，國家在2020年提出了“地?cái)偨?jīng)濟(jì)”．為響應(yīng)國家號召，有不少地區(qū)出臺了相關(guān)政策去鼓勵(lì)“地?cái)偨?jīng)濟(jì)”．某攤主2020年4月初向銀行借了免息貸款8000元，用于進(jìn)貨，因質(zhì)優(yōu)價(jià)廉，供不應(yīng)求，據(jù)測算：每月獲得的利潤是該月初投入資金的20%，每月底扣除生活費(fèi)800元，余款作為資金全部用于下月再進(jìn)貨，如此繼續(xù)，預(yù)計(jì)到2021年3月底該攤主的年所得收入為（　　）（取（1.2）¹¹=7.5，（1.2）¹²=9）

  A．24000元

  B．26000元

  C．30000元

  D．32000元
  組卷：134引用：5難度：0.6

  解析

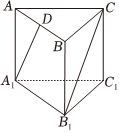• 7．直三棱柱ABC-A₁B₁C₁如圖所示，AB=4，BC=3，AC=5，D為棱AB的中點(diǎn)，三棱柱的各頂點(diǎn)在同一球面上，且球的表面積為61π，則異面直線A₁D和B₁C所成的角的余弦值為（　　）

  A． 3 2 5

  B． 2 5

  C． 4 2 5

  D． 16 2 25
  組卷：353引用：7難度：0.6

  解析

四、解答題（共70分）

• 21．已知函數(shù)f（x）=x²+（x-1）e^x．
  （1）求f（x）的極值；
  （2）當(dāng)x₂＞x₁≥1時(shí)，求證：

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  ＞

  4

  x

  1

  x

  2

  ．
  組卷：145引用：3難度：0.4

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  alnx

  -

  b

  e

  x

  x

  （a,b∈R且a≠0，e為自然對數(shù)的底數(shù)）．
  （1）若曲線f（x）在點(diǎn)x=e處的切線斜率為0，且f（x）有極小值，求實(shí)數(shù)a的取值范圍；
  （2）當(dāng)a=1，b=-1時(shí)，若不等式xf（x）＞e+m（x-1）在區(qū)間（1，+∞）內(nèi)恒成立，求實(shí)數(shù)m的最大值．
  組卷：18引用：1難度：0.5

  解析