2021-2022學年吉林省長春五中高二（下）期末數學試卷

一、單選題

• 1．A={x|x²-2x-3≥0}，

  B

  =

  {

  x

  ∈

  Z

  |

  x

  +

  2

  x

  -

  2

  ≤

  0

  }

  ，則A∩B=（　　）

  A．[-2，-1]

  B．[-1，2）

  C．{-2，-1}

  D．{-1，2}
  組卷：341引用：2難度：0.8

  解析

• 2．設a＜b＜0，給出下列四個結論：①a+b＜ab；②2a＜3b；③a²＜b²；④a|a|＜b|b|．其中正確的結論的序號為（　　）

  A．①②

  B．①④

  C．②③④

  D．①②③
  組卷：259引用：9難度：0.9

  解析

• 3．已知

  a

  =

  1

  2

  ，b=log₂3，

  c

  =

  lo

  g

  3

  1

  5

  ，則（　　）

  A．a＞c＞b

  B．c＞a＞b

  C．b＞a＞c

  D．a＞b＞c
  組卷：224引用：3難度：0.7

  解析

• 4．已知函數f（x）=x²-2kx+2k²-1（k∈R），則“對任意實數x,f（x）＞0恒成立”是“k＞1”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：138引用：2難度：0.6

  解析

• 5．函數

  f

  （

  x

  ）

  =

  （

  2

  1

  +

  e

  x

  -

  1

  ）

  sinx

  的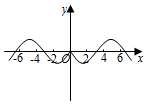圖象大致是（　　）

  A．

  B．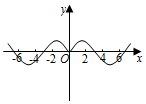

  C．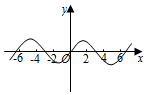

  D．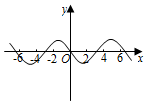
  組卷：231引用：20難度：0.9

  解析

• 6．若函數f（x）在R上可導，且f（x）=x²+2f′（2）x+m（m∈R），則（　　）

  A．f（0）＜f（6）	B．f（0）=f（6）
  C．f（0）＞f（6）	D．以上答案都不對
  組卷：178引用：4難度：0.7

  解析

• 7．2021年元旦期間，某高速公路收費站的四個高速收費口每天通過的小汽車數X_i（i=1，2，3，4）（單位：輛）均服從正態分布N（600，σ²），若

  P

  （

  500

  ＜

  X

  i

  ＜

  700

  ）

  =

  1

  3

  （

  i

  =

  1

  ，

  2

  ，

  3

  ，

  4

  ）

  ，假設四個收費口均能正常工作，則這四個收費口每天至少有一個不低于700輛小汽車通過的概率為（　　）

  A． 8 9

  B． 8 27

  C． 16 27

  D． 65 81
  組卷：256引用：5難度：0.6

  解析

四、解答題

• 21．已知函數f（x）=e^x+ax²-x.
  （1）當a=1時，討論f（x）的單調性；
  （2）當x≥0時，f（x）≥

  1

  2

  x³+1，求a的取值范圍．
  組卷：9338引用：23難度：0.3

  解析

• 22．已知函數f（x）=ae^x-1-lnx+lna.
  （1）當a=e時，求曲線y=f（x）在點（1，f（1））處的切線與兩坐標軸圍成的三角形的面積；
  （2）若f（x）≥1，求a的取值范圍．
  組卷：9576引用：30難度：0.2

  解析