2022-2023學年云南省昆明市行知中學高二（上）月考數學試卷（2月份）

一、單選題（本大題共8小題，共40分。在每小題列出的選項中，選出符合題目的一項）

• 1．已知集合A={x|2≤x＜4}，集合B={x|x²-3x+2＜0}，則A∪B=（　　）

  A．?

  B．{x|1＜x＜2}

  C．{x|2≤x＜4}

  D．{x|1＜x＜4}
  組卷：235引用：8難度：0.8

  解析

• 2．復數z=

  5

  i

  1

  -

  2

  i

  的共軛復數的模是（　　）

  A． 2 5

  B． 5

  C． 2 5 5

  D． 5 5
  組卷：23引用：3難度：0.7

  解析

• 3．設S_n為等差數列{a_n}的前n項和，若a₄+a₅=12，則S₈的值為（　　）

  A．14

  B．28

  C．36

  D．48
  組卷：807引用：9難度：0.8

  解析

• 4．設隨機變量X服從兩點分布，若P（X=1）-P（X=0）=0.4，則E（X）=（　　）

  A．0.3

  B．0.4

  C．0.6

  D．0.7
  組卷：243引用：7難度：0.6

  解析

• 5．藥物在體內的轉運及轉化形成了藥物的體內過程，從而產生了藥物在不同器官、組織、體液間的濃度隨時間變化的動態過程，根據這種動態變化過程建立兩者之間的函數關系，可以定量反映藥物在體內的動態變化，為臨床制定和調整給藥方案提供理論依據，經研究表明，大部分注射藥物的血藥濃度C（t）（單位：μg/mL）隨時間t（單位：h）的變化規律可近似表示為C（t）=C₀?e^-kt，其中C₀表示第一次靜脈注射后人體內的初始血藥濃度，k表示該藥物在人體內的消除速率常數．已知某麻醉藥的消除速率常數k=0.5（單位：h^-1），某患者第一次靜脈注射該麻醉藥后即進入麻醉狀態，測得其血藥濃度為4.5μg/mL，當患者清醒時測得其血藥濃度為0.9μg/mL，則該患者的麻醉時間約為（　　）（ln5≈1.609）

  A．3.5h

  B．3.2h

  C．2.2h

  D．0.8h
  組卷：158引用：4難度：0.9

  解析

• 6．若非零向量

  a

  ，

  b

  滿足|

  a

  |=3|

  b

  |，（2

  a

  +3

  b

  ）⊥

  b

  ，則

  a

  與

  b

  的夾角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：937引用：16難度：0.8

  解析

• 7．已知拋物線C：y²=2px,直線l經過焦點F交C于A，B兩點，其中點A的坐標為（4，4），則|AB|=（　　）

  A． 15 4

  B．5

  C．6

  D． 25 4
  組卷：51引用：1難度：0.5

  解析

四、解答題（本大題共6小題，共70分。解答應寫出文字說明，證明過程或演算步驟）

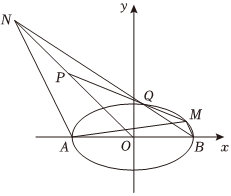• 21．如圖所示，A，B為橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右頂點，離心率為

  3

  2

  ，且經過點

  （

  3

  ，

  1

  2

  ）

  ．
  （1）求橢圓C的方程；
  （2）已知O為坐標原點，點P（-2，2），點M是橢圓C上的點，直線PM交橢圓C于點Q（M，Q不重合），直線BQ與OP交于點N．求證：直線AM，AN的斜率之積為定值，并求出該定值．
  組卷：210引用：6難度：0.5

  解析

• 22．已知函數f（x）=4lnx-ax+

  a

  +

  3

  x

  （a≥0）．
  （1）當a=

  1

  2

  ，求f（x）的極值．
  （2）當a≥1時，設g（x）=2e^x-4x+2a,若存在x₁，x₂∈[

  1

  2

  ，2]，使f（x₁）＞g（x₂），求實數a的取值范圍．（e為自然對數的底數，e=2.71828…）
  組卷：175引用：9難度：0.5

  解析