當前位置：試卷中心 > 試卷詳情

2021-2022學年廣西南寧市普通高中聯盟高二（上）期末數學試卷（理科）

發布：2024/4/20 14:35:0

1．已知等比數列{a_n}中，a₂=2，a₅=16，則該數列的公比為（　　）
A．-3 B．-2 C．2 D．3
組卷：206引用：3難度：0.7
解析
2．不等式（x+2）（x-3）＞0的解集是（　　）
A．{x|x＜-2，或x＞3} B．{x|-2＜x＜3}
C．{x|2＜x＜3} D．R
組卷：149引用：4難度：0.9
解析
3．橢圓
x
2
16
+
y
2
4
=
1
的長軸長為（　　）
A．2 B．4 C．8 D．16
組卷：102引用：6難度：0.7
解析
4．已知△ABC中，內角A、B、C所對的邊分別a,b,c,若a=1，b=2，
sin
A
=
1
6
，則sinB=（　　）
A．
2
3
B．
1
3
C．
5
6
D．
1
2
組卷：411引用：11難度：0.8
解析
5．若命題p為真命題，命題q為假命題，則以下為真命題的是（　　）
A．p∧q B．p∧（￢q） C．（￢p）∨q D．（￢p）∧（￢q）
組卷：135引用：12難度：0.9
解析
6．已知三維數組
a
=（2，-1，0），
b
=（1，k,7），且
a
?
b
=0，則實數k=（　　）
A．-2 B．-9 C．
2
7
D．2
組卷：184引用：3難度：0.9
解析
7．已知p：0＜x＜1，那么p的一個充分不必要條件是（　　）
A．1＜x＜3 B．-1＜x＜1 C．
1
3
＜
x
＜
3
4
D．
1
2
＜
x
＜
5
組卷：139引用：2難度：0.7
解析

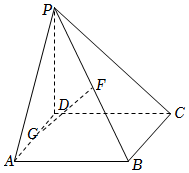21．如圖，在四棱錐P-ABCD中，PD⊥底面ABCD，底面ABCD是邊長為2的正方形，PD=DC，F，G分別是PB，AD的中點．
（1）求證：GF⊥平面PCB；
（2）求二面角A-PB-C的大小；
組卷：106引用：3難度：0.6
解析
22．已知點A（0，-2），橢圓E：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的離心率為
3
2
，F是橢圓E的右焦點，直線AF的斜率為
2
3
3
，O為坐標原點．設過點A的動直線l與E相交于P，Q兩點．
（1）求E的方程；
（2）是否存在這樣的直線l,使得△OPQ的面積為
4
5
，若存在，求出l的方程；若不存在，請說明理由．
組卷：214引用：6難度：0.7
解析