2022-2023學年山東省青島二中分校高二（上）期中數學試卷

一、選擇題。（本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

• 1．圓x²+y²+2x-4y-6=0的圓心和半徑分別是（　　）

  A．（-1，-2），11

  B．（-1，2），11

  C．（-1，-2）， 11

  D．（-1，2）， 11
  組卷：765引用：17難度：0.9

  解析

• 2．直線x+

  3

  y+1=0的傾斜角是（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：1201引用：32難度：0.9

  解析

• 3．點P（2，0）關于直線l：x+y+1=0的對稱點Q的坐標為（　　）

  A．（-1，-3）

  B．（-1，-4）

  C．（4，1）

  D．（2，3）
  組卷：692引用：15難度：0.8

  解析

• 4．已知

  a

  =

  （

  2

  ，-

  2

  ，-

  3

  ）

  ，

  b

  =

  （

  2

  ，

  0

  ，

  4

  ）

  ，則

  cos

  ?

  a

  ，

  b

  ?

  =（　　）

  A． 4 85 85

  B． - 4 85 85

  C．0

  D．1
  組卷：998引用：12難度：0.8

  解析

• 5．已知兩點A（-3，2），B（2，1），過點P（0，-1）的直線與線段AB有交點，則直線l的傾斜角的取值范圍為（　　）

  A．[ π 4 ， 3 π 4 ]	B．[0， π 4 ]∪[ π 2 ， 3 π 4 ]
  C．[0， π 2 ]∪[ 3 π 4 ，π]	D．[ π 4 ， π 2 ）∪（ π 2 ， 3 π 4 ]
  組卷：644引用：6難度：0.5

  解析

• 6．已知直線l：x-y+4=0與圓C：（x-1）²+（y-1）²=2，則C上各點到l距離的最小值為（　　）

  A． 2 -1

  B． 2 +1

  C． 2

  D．2 2
  組卷：254引用：9難度：0.9

  解析

• 7．已知F₁，F₂是橢圓C：

  x

  2

  9

  +

  y

  2

  4

  =1的兩個焦點，點M在C上，則|MF₁|?|MF₂|的最大值為（　　）

  A．13

  B．12

  C．9

  D．6
  組卷：9729引用：52難度：0.7

  解析

四、解答題。（共70分）

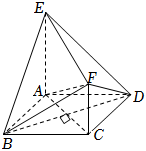• 21．如圖，EA⊥平面ABCD，EA∥FC，AC=EA=2FC=2，四邊形ABCD為菱形．
  （1）證明：FA⊥平面EBD；
  （2）若直線AB與平面EBD所成角的正弦值為

  2

  5

  ，求三棱錐E-BDF的體積．
  組卷：139引用：7難度：0.6

  解析

• 22．已知圓C經過坐標原點O，圓心在x軸正半軸上，且與直線3x+4y-8=0相切．
  （1）求圓C的標準方程．
  （2）直線l：y=kx+2與圓C交于A，B兩點．
  （ⅰ）求k的取值范圍；
  （ⅱ）證明：直線OA與直線OB的斜率之和為定值．
  組卷：937引用：11難度：0.5

  解析