2021-2022學(xué)年江蘇省淮安市高一（下）期末數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

• 1．設(shè)i為虛數(shù)單位，若復(fù)數(shù)（1-i）（1+ai）是實(shí)數(shù)，則實(shí)數(shù)a的值為（　　）

  A．-1

  B．0

  C．1

  D．2
  組卷：174引用：4難度：0.8

  解析

• 2．在△ABC中，a,b,c分別是角A，B，C的對(duì)邊，若a=ccosB，則△ABC的形狀（　　）

  A．銳角三角形

  B．直角三角形

  C．鈍角三角形

  D．不能確定
  組卷：117引用：1難度：0.7

  解析

• 3．用半徑為2的半圓形鐵皮圍成一個(gè)圓錐筒，則該圓錐筒的高為（　　）

  A．1

  B． 3

  C．2

  D．6
  組卷：110引用：2難度：0.8

  解析

• 4．“哥德巴赫猜想”是近代三大數(shù)學(xué)難題之一，其內(nèi)容是：一個(gè)大于2的偶數(shù)都可以寫(xiě)成兩個(gè)質(zhì)數(shù)（也稱(chēng)為素?cái)?shù)，是一個(gè)大于1的自然數(shù)，除了1和它自身之外，不能被其它自然數(shù)整除的數(shù)叫做質(zhì)數(shù)）之和，也就是我們所謂的“1+1”問(wèn)題．它是1742年由數(shù)學(xué)家哥德巴赫提出的，我國(guó)數(shù)學(xué)家潘承洞、王元、陳景潤(rùn)等曾在哥德巴赫猜想的證明中做出過(guò)相當(dāng)好的成績(jī)．若將6拆成兩個(gè)正整數(shù)的和（不考慮兩個(gè)加數(shù)的順序），則加數(shù)全部為質(zhì)數(shù)的概率是（　　）

  A． 1 3

  B． 1 4

  C． 1 2

  D． 1 6
  組卷：69引用：2難度：0.8

  解析

• 5．在△ABC中，B=45°，點(diǎn)D是邊BC上一點(diǎn)，AD=5，AC=7，DC=3，則邊AB的長(zhǎng)是（　　）

  A． 4 6

  B． 10 3 6

  C． 5 6 2

  D． 2 6
  組卷：141引用：1難度：0.7

  解析

• 6．已知

  e

  1

  ，

  e

  2

  是平面內(nèi)的一組基底，

  OA

  =3

  e

  1

  +2

  e

  2

  ，

  OB

  =4

  e

  1

  +k

  e

  2

  ，

  OC

  =5

  e

  1

  -4

  e

  2

  ，若A，B，C三點(diǎn)共線，則實(shí)數(shù)k的值為（　　）

  A．-1

  B．0

  C．1

  D．2
  組卷：187引用：2難度：0.8

  解析

• 7．甲、乙兩名籃球運(yùn)動(dòng)員在隨機(jī)抽取的12場(chǎng)比賽中的得分情況如下：
  甲：12，15，20，25，31，31，36，36，37，39，44，49；
  乙：8，13，14，16，23，26，28，29，31，38，39，51．
  則運(yùn)動(dòng)員甲得分的25百分位數(shù)與運(yùn)動(dòng)員乙得分的80百分位數(shù)的和為（　　）

  A．22.5

  B．38

  C．60.5

  D．39
  組卷：132引用：2難度：0.8

  解析

四、解答題：本題共6小題，共70分。解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟。

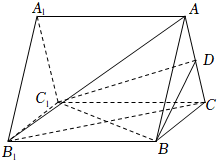• 21．如圖，在正三棱柱ABC-A₁B₁C₁中，點(diǎn)D為AC中點(diǎn)．
  （1）若AB=AA₁，證明：平面AA₁C₁C⊥平面DBC₁；
  （2）若AB=2，且二面角D-BC₁-C的正切值為

  15

  6

  ，求三棱柱ABC-A₁B₁C₁的體積．
  組卷：289引用：1難度：0.6

  解析

• 22．在①2acosA=bcosC+ccosB；②

  tan

  B

  +

  tan

  C

  +

  3

  =

  3

  tan

  B

  tan

  C

  這兩個(gè)條件中任選一個(gè)，補(bǔ)充在下面的問(wèn)題中，并加以解答．
  在△ABC中，a,b,c分別是角A，B，C的對(duì)邊，已知_____．
  （1）求角A的大小；
  （2）若△ABC為銳角三角形，且其面積為

  3

  2

  ，點(diǎn)G為△ABC重心，點(diǎn)M為線段AC的中點(diǎn)，點(diǎn)N在線段AB上，且AN=2NB，線段BM與線段CN相交于點(diǎn)P，求

  |

  GP

  |

  的取值范圍．
  注：如果選擇多個(gè)方案分別解答，按第一個(gè)方案解答計(jì)分．
  組卷：204引用：5難度：0.5

  解析