2022-2023學年北京市石景山區(qū)高一（上）期末數(shù)學試卷

一、選擇題共10小題，每小題4分，共40分．在每小題列出的四個選項中，選出符合題目要求的一項。

• 1．設命題p：?n∈N，n²＞2ⁿ，則￢p為（　　）

  A．?n∈N，n2＞2n

  B．?n∈N，n2≤2n

  C．?n∈N，n2≤2n

  D．?n∈N，n2=2n
  組卷：6485引用：183難度：0.9

  解析

• 2．不等式

  2

  x

  -

  1

  ≥

  1

  的解集為（　　）

  A．（-∞，1]∪[3，+∞）	B．[1，3]
  C．（-∞，1）∪[3，+∞）	D．（1，3]
  組卷：217引用：2難度：0.7

  解析

• 3．擲兩顆均勻的骰子，則點數(shù)之和為5的概率等于（　　）

  A． 1 18

  B． 1 9

  C． 1 6

  D． 1 12
  組卷：2242引用：37難度：0.9

  解析

• 4．在同一直角坐標系中，函數(shù)f（x）=x^a（x＞0），g（x）=log_ax的圖象可能是（　　）

  A．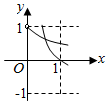

  B．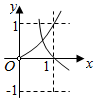

  C．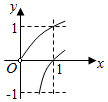

  D．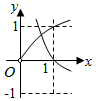
  組卷：2129引用：74難度：0.7

  解析

• 5．已知a、b、c都是實數(shù)，則“a＜b”是“ac²＜bc²”的（　　）

  A．充分非必要條件	B．必要非充分條件
  C．充要條件	D．既非充分也非必要條件
  組卷：445引用：15難度：0.8

  解析

• 6．若a＞b＞0，0＜c＜1，則（　　）

  A．logac＜logbc	B．logca＜logcb
  C．a(chǎn)c＜bc	D．ca＞cb
  組卷：8796引用：32難度：0.9

  解析

三、解答題共5小題，共35分．解答應寫出文字說明，演算步驟或證明過程。

• 19．已知函數(shù)f（x）=log₂

  1

  +

  ax

  x

  -

  1

  （a為常數(shù)）是奇函數(shù)．
  （Ⅰ）求a的值與函數(shù) f（x）的定義域；
  （Ⅱ）若當x∈（1，+∞） 時，f（x）+log₂（x-1）＞m恒成立．求實數(shù)m的取值范圍．
  組卷：1042引用：18難度：0.3

  解析

• 20．甲、乙兩人進行羽毛球比賽，采取“三局兩勝”制，即兩人比賽過程中，誰先勝兩局即結束比賽，先勝兩局的是勝方，另一方是敗方．根據(jù)以往的數(shù)據(jù)分析，每局比賽甲勝乙的概率均為

  3

  5

  ，甲、乙比賽沒有平局，且每局比賽是相互獨立的．
  （1）求比賽恰進行兩局就結束的概率；
  （2）求這場比賽甲獲勝的概率．
  組卷：612引用：4難度：0.8

  解析