2018-2019學年重慶外國語學校九年級（下）開學數學試卷

一、選擇題（本大題共12個小題，每小題4分，共48分）在每個小題的下面，都給出了代號為A,B,C,D的四個答案，其中只有一個是正確的，請將正確的答案的代號在答題卡中對應的方框涂黑。

• 1．四個實數0、

  1

  3

  、-3.14、-2中，最小的數是（　　）

  A．0

  B． 1 3

  C．-3.14

  D．-2
  組卷：150引用：5難度：0.9

  解析

• 2．下列汽車標志中，可以看作是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：340引用：50難度：0.9

  解析

• 3．下列調查方式中適合的是（　　）

  A．為了了解市民對電影《南京南京》的感受，小華在某校隨機采訪了8名初三學生

  B．為了了解全校學生用于做數學作業的時間，小民同學在網上向3位好友做了調查

  C．為了了解某段水域的水質情況，環保部門采用了抽樣調查的方式

  D．為了了解全市中學生每天的就寢時間，調查人員采用了普查的方式
  組卷：163引用：1難度：0.8

  解析

• 4．觀察下列圖中所示的一系列圖形，它們是按一定規律排列的，依照此規律，第2019個圖形共有（　　）個〇．
  

  A．6055

  B．6056

  C．6057

  D．6058
  組卷：579引用：6難度：0.8

  解析

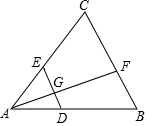• 5．如圖，在△ABC中，D、E分別為AB、AC邊上的點，DE∥BC，點F為BC邊上一點，連接AF交DE于點G，則下列結論中一定正確的是（　　）

  A． AD AB = AE EC

  B． AG GF = AE BD

  C． BD AD = CE AE

  D． AG AF = AC EC
  組卷：3048引用：33難度：0.7

  解析

• 6．下列命題是真命題的有（　　）個
  ①一組對邊相等的四邊形是矩形；②兩條對角線相等的四邊形是矩形；③四條邊都相等且對角線互相垂直的四邊形是正方形；④四條邊都相等的四邊形是菱形；⑤一組鄰邊相等的矩形是正方形．

  A．1

  B．2

  C．3

  D．4
  組卷：157引用：2難度：0.6

  解析

• 7．估計

  11

  （2

  11

  -1）的值應在（　　）

  A．16和17之間

  B．17和18之間

  C．18和19之間

  D．20和21之間
  組卷：166引用：2難度：0.8

  解析

• 8．小明按如圖所示的程序輸入一個正數x,最后輸出的結果為597，則滿足條件的x的不同值最多有（　　）
  

  A．4個

  B．5個

  C．6個

  D．無數個
  組卷：245引用：2難度：0.8

  解析

五、解答題（本大題2個小題,25題10分,26題12分,共22分)解答時每小題都必須寫出必要的演算過程成推理步驟,請將解答過程書寫在答題卡中對應的位置上。

• 25．我國著名的數學家秦九韶在《數書九章》提出了“三斜求積術”．即已知三角形的三邊長，求它的面積．
  用現代式子表示即為s=

  1

  4

  [

  a

  2

  b

  2

  -

  （

  a

  2

  +

  b

  2

  -

  c

  2

  2

  ）

  2

  ]

  ……①（其中a,b,c為三角形的三邊長，s為面積．）
  而另一個文明古國古希臘也有求三角形面積的海倫公式：
  s=

  p

  （

  p

  -

  a

  ）

  （

  p

  -

  b

  ）

  （

  p

  -

  c

  ）

  …②（其中a,b,c為三角形的三邊長，p=

  a

  +

  b

  +

  c

  2

  ）
  （1）若已知三角形的三邊長分別為5、7、8，請在上述兩種公式中選擇一種你喜歡的公式，計算該三角形的面積；
  （2）事實上，“三斜求積術”與海倫公式是等價的，可以由“三斜求積術”直接推導出海倫公式，其部分推導過程如下：
  ∵

  1

  4

  [a²b²-（

  a

  2

  +

  b

  2

  -

  c

  2

  2

  ）²]=

  1

  16

  [4a²b²-（a²+b²-c²）²]
  =…
  請將上述推導過程補充完整；
  （3）如圖，已知A、B是線段MN上的兩點，MN=4，MA=1，MB＞1，以A為中心順時針旋轉點M，以B為中心逆時針旋轉點N，使M、N兩點重合成一點C，構成△ABC，設AB=x,試利用海倫公式求△ABC的最大面積．
  
  組卷：289引用：1難度：0.4

  解析

• 26．二次函數y=-

  3

  6

  x²

  +

  3

  2

  x

  +

  2

  3

  圖象與x軸交于A、B兩點，與y軸交于點C，連接AC、BC．
  （1）如圖1，求△ABC的周長；
  （2）如圖2，D為線段AB上一動點，作DE∥BC交AC于點E，當△CDE面積最大時，過E作x軸的平行線，交y軸于點F，交BC于點H，點P為線段FH上一動點，將△CFH繞點C沿逆時針方向旋轉90°，點F，P，H的對應點分別是F′，P′，H′，點Q從點P出發，先沿適當的路徑運動到點F′處，再沿F′C運動到點C處，最后沿適當的路徑運動到點P′處停止，求點Q經過的最短路徑的長是多少；
  （3）如圖3，點M是點C關于x軸的對稱點，N是線段OB上一動點，經過MN的直線與拋物線交于點G，將△AMG沿MN翻折，點A的對應點是A′，是否存在點A′，使得△CBA′是等腰三角形，若存在求出點A′的坐標，若不存在，請說明理由．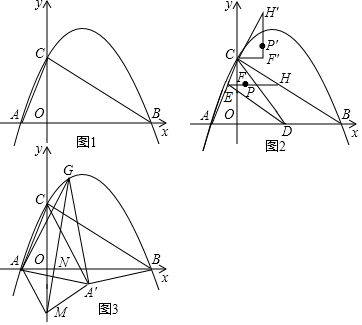
  
  組卷：534引用：2難度：0.1

  解析