2022年浙江省寧波市慈溪中學(xué)高考數(shù)學(xué)模擬試卷（5月份）

一、選擇題（本大題共10小題，每小題4分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

• 1．已知集合A={x||x|＜2}，B={x|x²-3x＜0}，則A∩B=（　　）

  A．（0，2）

  B．（0，3）

  C．（2，3）

  D．（-2，3）
  組卷：257引用：6難度：0.8

  解析

• 2．已知復(fù)數(shù)z滿足z（2-i）=a+i（其中a為實數(shù)，i為虛數(shù)單位）．若z∈R，則實數(shù)a=（　　）

  A．-2

  B． - 1 2

  C． 1 2

  D．2
  組卷：41引用：2難度：0.8

  解析

• 3．設(shè)α，β為兩個不同平面，直線m?α，則“α∥β”是“m∥β”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：187引用：22難度：0.9

  解析

• 4．某幾何體的三視圖如圖所示，則該幾何體的體積為（　　）

  A． 16 3 3

  B． 8 3

  C． 16 3

  D． 40 3 3
  組卷：68引用：2難度：0.7

  解析

• 5．已知實數(shù)x,y滿足

  y ≤ 2

  x + y ≥ 4

  x - y ≤ 1

  ，則2x+y的最小值為（　　）

  A．4

  B．6

  C．8

  D．10
  組卷：37引用：3難度：0.7

  解析

• 6．已知函數(shù)f（x）=2^x，g（x）=sinx,則圖像為下列圖示的函數(shù)可能是（　　）

  A．y=[f（x）+f（-x）]?g（x）	B． y = g （ x ） f （ x ） + f （ - x ）
  C．y=[f（x）-f（-x）]?g（x）	D． y = g （ x ） f （ x ） - f （ - x ）
  組卷：115引用：2難度：0.7

  解析

• 7．在直角坐標系xOy中，已知點A，B分別是定直線y=kx和y=-kx（k＞0）上的動點，若△AOB的面積為定值S，則線段AB的中點的軌跡為（　　）

  A．圓

  B．橢圓

  C．雙曲線

  D．拋物線
  組卷：42引用：3難度：0.6

  解析

三、解答題（本大題共5小題，共74分．浙江省高中數(shù)學(xué)解答應(yīng)寫出文字說明、證明過程或演算步驟）

• 21．已知橢圓C₁：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的離心率為

  e

  =

  1

  2

  ，且過點

  P

  （

  -

  1

  ，

  3

  2

  ）

  ．點P到拋物線C₂：y²=-2px（p＞0）的準線的距離為

  3

  2

  ．
  （1）求橢圓C₁和拋物線C₂的方程；
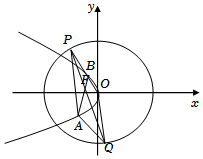
  （2）如圖過拋物線C₂的焦點作F作斜率為k（k＞0）的直線交拋物線C₂于A，B兩點（點A在x軸下方），直線PF交橢圓C₁于另一點Q記△FBQ，△APQ的面積分別記為S₁、S₂．當(dāng)PF恰好平分∠APB時，求

  S

  1

  S

  2

  的值．
  組卷：443引用：5難度：0.2

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  e

  x

  +

  a

  x

  2

  -

  e

  2

  x

  （a∈R）．
  （1）若函數(shù)

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  +

  （

  e

  2

  -

  1

  ）

  x

  在[0，+∞）上單調(diào)遞增，求實數(shù)a的最小值；
  （2）若函數(shù)f（x）在（0，1）上有兩個極值點x₁，x₂（x₁＜x₂）．
  （ⅰ）求實數(shù)a的取值范圍；
  （ⅱ）求證：

  （

  x

  1

  -

  e

  4

  a

  +

  1

  ）

  （

  x

  2

  -

  e

  4

  a

  +

  1

  ）

  ＞

  4

  ．
  組卷：135引用：2難度：0.3

  解析