2022-2023學(xué)年浙江省臺(tái)州市臨海市九年級(jí)（上）期末數(shù)學(xué)試卷

一、選擇題（本大題共10小題，每小題4分，共40分。請(qǐng)選出各題中一個(gè)符合題意的正確選項(xiàng)，不選、多選、錯(cuò)選，均不給分）

• 1．志愿服務(wù)，傳遞愛心，傳遞文明，下列志愿服務(wù)標(biāo)志為中心對(duì)稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：1019引用：21難度：0.9

  解析

• 2．某路口紅綠燈的時(shí)間設(shè)置如下：綠燈60秒，紅燈40秒，黃燈3秒，當(dāng)車隨機(jī)經(jīng)過該路口，遇到哪一種燈的可能性最大（　　）

  A．綠燈

  B．紅燈

  C．黃燈

  D．不能確定
  組卷：354引用：4難度：0.7

  解析

• 3．已知點(diǎn)A在半徑為2cm的圓內(nèi)，則點(diǎn)A到圓心的距離可能是（　　）

  A．1cm

  B．2cm

  C．3cm

  D．4cm
  組卷：463引用：6難度：0.5

  解析

• 4．下列事件是必然事件的是（　　）

  A．拋擲一枚硬幣，正面向上

  B．?dāng)S一次骰子，向上一面的點(diǎn)數(shù)是7

  C．在只有紅球的袋中，摸出一個(gè)紅球

  D．運(yùn)動(dòng)員射擊一次，命中靶心
  組卷：269引用：9難度：0.9

  解析

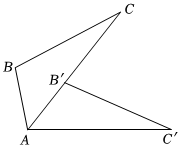• 5．如圖，將△ABC繞點(diǎn)A順時(shí)針旋轉(zhuǎn)一定的角度得到△AB′C′，此時(shí)點(diǎn)B′恰在邊AC上，若AB=2，AC′=5，則B′C的長(zhǎng)為（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：1273引用：13難度：0.5

  解析

• 6．若x=1是關(guān)于x的一元二次方程x²+mx+2=0的一個(gè)解，則另一個(gè)解為（　　）

  A．x=-1

  B．x=-2

  C．x=1

  D．x=2
  組卷：156引用：2難度：0.5

  解析

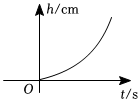• 7．小明向各種空水壺內(nèi)勻速注水，壺內(nèi)水的深度h（單位：cm）與注水時(shí)間t（單位：s）的函數(shù)關(guān)系如圖所示，選項(xiàng)中是各種水壺的平面圖，則小明使用的水壺是（　　）

  A．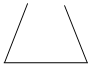

  B．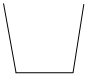

  C．

  D．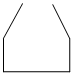
  組卷：1105引用：7難度：0.5

  解析

• 8．我國(guó)古代數(shù)學(xué)家楊輝的《田畝比數(shù)乘除減法》中記載：“直田積八百六十四步，只云闊不及長(zhǎng)一十二步，問闊及長(zhǎng)各幾步？”翻譯成數(shù)學(xué)問題是：一塊矩形田地的面積為864平方步，它的寬比長(zhǎng)少12步．如果設(shè)寬為x步，則可列出方程（　　）

  A．x（x-6）=864	B．x（x-12）=864
  C．x（x+6）=864	D．x（x+12）=864
  組卷：419引用：15難度：0.5

  解析

三、解答題（本題有8小題，第17～20題每題8分，第21題10分，第22，23題每題12分，第24題14分，共80分）

• 23．如圖1，為美化校園，學(xué)校要建造一個(gè)圓形噴水池，計(jì)劃在噴水池周邊安裝一圈可移動(dòng)的噴水頭向中央噴水，使水流沿形狀相同的拋物線落下．以噴水池中心為原點(diǎn)，水平方向?yàn)閤軸、中心線為y軸建立平面直角坐標(biāo)系，則水柱高度y（單位：m）與水柱距離噴水池中心的水平距離x（單位：m）之間的關(guān)系如圖2所示．當(dāng)水流與中心線的水平距離為2m時(shí)，達(dá)到最大高度3.61m,此時(shí)水柱剛好經(jīng)過中心線上的點(diǎn)A，已知點(diǎn)A距水面高2.61m.
  （1）求如圖2所示拋物線的解析式．
  （2）為形成錯(cuò)落有致的噴水景觀，現(xiàn)讓噴水頭向中心線沿直線滑動(dòng)，在保持水流形狀不變的情況下，要求噴水柱最高點(diǎn)不能超過中心線，若噴水頭的位置用（p,0）表示．（僅考慮y軸右側(cè)的情況）．
  ①求p的取值范圍；
  ②若水剛好噴到中心線上，且距水面高3.25m處，直接寫出此時(shí)p的值

  ．
  組卷：1193引用：5難度：0.5

  解析

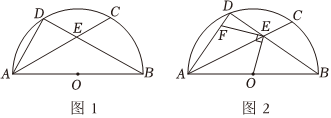• 24．如圖，AB是⊙O的直徑，AB=10，點(diǎn)D是半圓上的動(dòng)點(diǎn)，點(diǎn)C是

  ?

  BD

  中點(diǎn)，AC，BD交于點(diǎn)E，連接AD．
  （1）如圖1，若∠ABD=30°，
  ①則∠CAD的度數(shù)為

  ；
  ②求點(diǎn)E到AB的距離．
  （2）如圖2，連接EO，將EO繞點(diǎn)E順時(shí)針旋轉(zhuǎn)90°，點(diǎn)O的對(duì)應(yīng)點(diǎn)F恰好落在AD上，求證：OB=EB．
  （3）在（2）的條件下，連接BC并延長(zhǎng)，交AD的延長(zhǎng)線于點(diǎn)G，直接寫出四邊形CEDG的面積

  ．
  組卷：400引用：4難度：0.2

  解析