2022年安徽省合肥五中高考數學模擬試卷（一）（理科）

一、選擇題（本大題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

• 1．若集合A={x|x²+5x+4＜0}，集合B={x|x＜-2}，則A∩（?_RB）等于（　　）

  A．（-2，-1）

  B．[-2，4）

  C．[-2，-1）

  D．?
  組卷：85引用：3難度：0.9

  解析

• 2．命題p：|x+2|＞2，命題q：

  1

  3

  -

  x

  ＞1，則￢q是￢p成立的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：358引用：23難度：0.9

  解析

• 3．已知命題p：“?x＞0，都有3^x＞1”的否定是“?x≤0，使3^x≤1”；
  命題q：“a,b∈R，若a²+b²=0，則a=b=0”的否命題是“a,b∈R，若a²+b²≠0，則a≠0或b≠0”；
  下列命題為真命題的是（　　）

  A．p∧q

  B．p∨（￢q）

  C．（￢p）∧q

  D．（￢p）∧（￢q）
  組卷：88引用：2難度：0.8

  解析

• 4．函數

  f

  （

  x

  ）

  =

  2

  sinx

  1

  -

  |

  x

  |

  的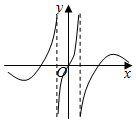圖象大致是（　　）

  A．

  B．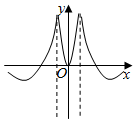

  C．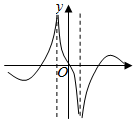

  D．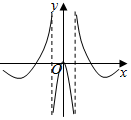
  組卷：454引用：5難度：0.6

  解析

• 5．已知（1+ax）⁵=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵，若a₃=-80，則a₁+a₂+a₃+a₄+a₅=（　　）

  A．1

  B．0

  C．-1

  D．-2
  組卷：350引用：2難度：0.6

  解析

• 6．若實數x,y滿足約束條件

  x - 2 ≥ 0 ，

  2 x + y - 7 ≤ 0 ，

  x - y - 2 ≤ 0 ，

  則z=3x+4y的最大值是（　　）

  A．20

  B．18

  C．13

  D．6
  組卷：490引用：3難度：0.7

  解析

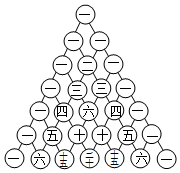• 7．楊輝三角，又稱帕斯卡三角，是二項式系數在三角形中的一種幾何排列．在我國南宋數學家楊輝所著的《詳解九章算法》（1261年）一書中用如圖所示的三角形解釋二項式乘方展開式的系數規律．現把楊輝三角中的數從上到下，從左到右依次排列，得數列：1，1，1，1，2，1，1，3，3，1，1，4，6，4，1……．記作數列{a_n}，若數列{a_n}的前n項和為S_n，則S₄₇=（　　）

  A．265

  B．521

  C．1034

  D．2059
  組卷：178引用：8難度：0.5

  解析

[選修4-4：坐標系與參數方程]

• 22．在平面直角坐標系xOy中，以原點為極點，x軸的非負半軸為極軸建立極坐標系，并在兩個坐標系下取相同的長度單位，已知曲線C的參數方程為

  x = 1 + 3 cosθ

  y = 3 sinθ

  （θ為參數），直線l的參數方程為

  x = 2 + tcosα

  y = 1 + tsinα

  （t為參數，α為直線l的傾斜角）．
  （1）求曲線C的普通方程；當α=

  π

  3

  時，求直線l的極坐標方程；
  （2）若曲線C和直線l交于M，N兩點，且|MN|=

  10

  ，求直線l的傾斜角．
  組卷：160引用：5難度：0.6

  解析

[選修4-5：不等式選講]

• 23．設函數f（x）=|x-m|+|x+n|，其中m＞0，n＞0．
  （1）當m=1，n=1時，求關于x的不等式f（x）≥4的解集；
  （2）若m+n=mn,證明：f（x）≥4．
  組卷：69引用：5難度：0.7

  解析