2022-2023學年江蘇省宿遷市高二（下）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每個小題給出的四個選項中，只有一項是符合題目要求的．

• 1．設n∈N₊，化簡

  C

  0

  n

  +

  C

  1

  n

  6

  1

  +

  C

  2

  n

  6

  2

  +

  C

  3

  n

  6

  3

  +

  ?

  +

  C

  n

  n

  6

  n

  =（　　）

  A．6n

  B．6n-1

  C．7n

  D．7n-1
  組卷：50引用：1難度：0.8

  解析

• 2．已知平面α的一個法向量為

  n

  =

  （

  1

  ，-

  1

  ，

  2

  ）

  ，

  AB

  =

  （

  -

  1

  ，

  1

  ，-

  2

  ）

  ，則AB所在直線l與平面α的位置關系為（　　）

  A．l⊥α	B．l?α
  C．l∥α	D．l與α相交但不垂直
  組卷：98引用：5難度：0.7

  解析

• 3．已知向量

  a

  =

  （

  0

  ，

  1

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ，

  0

  ）

  ，則向量

  b

  在向量

  a

  上的投影向量為（　　）

  A．（0，-1，-1）

  B．（-1，0，-1）

  C． （ 0 ， 1 2 ， 1 2 ）

  D． （ 1 2 ， 0 ， 1 2 ）
  組卷：212引用：8難度：0.8

  解析

• 4．由0，1，2，3，5組成的無重復數字的五位偶數共有（　　）

  A．36個

  B．42個

  C．48個

  D．120個
  組卷：264引用：8難度：0.9

  解析

• 5．已知空間四面體OABC中，對空間內任一點M，滿足

  OM

  =

  1

  4

  OA

  +

  1

  6

  OB

  +

  λ

  OC

  ，下列條件中能確定點M，A，B，C共面的是（　　）

  A． λ = 1 2

  B． λ = 1 3

  C． λ = 5 12

  D． λ = 7 12
  組卷：575引用：5難度：0.7

  解析

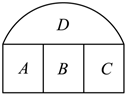• 6．如圖，提供4種不同的顏色給圖中A，B，C，D四塊區域涂色，若相鄰的區域不能涂同一種顏色，則不同的涂法共有（　　）種

  A．12

  B．36

  C．48

  D．72
  組卷：235引用：4難度：0.5

  解析

• 7．當n∈N時，將三項式（x²+x+1）ⁿ展開，可得到如圖所示的三項展開式和“廣義楊輝三角形”：
  （x²+x+1）⁰=1
  （x²+x+1）¹=x²+x+1
  （x²+x+1）²=x⁴+2x³+3x²+2x+1
  （x²+x+1）³=x⁶+3x⁵+6x⁴+7x³+6x²+3x+1
  （x²+x+1）⁴=x⁸+4x⁷+10x⁶+16x⁵+19x⁴+16x³+10x²+4x+1
  ……
  
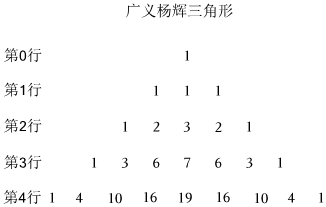
  若在（1+ax）（x²+x+1）⁵的展開式中，x⁸的系數為75，則實數a的值為（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：88引用：2難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．（1）3個不同的小球放入編號為1，2，3，4的4個盒子中，一共有多少種不同的放法？
  （2）3個不同的小球放入編號為1，2，3，4的4個盒子中，恰有2個空盒的放法共有多少種？
  組卷：205引用：3難度：0.8

  解析

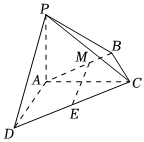• 22．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BCA=60°，AP=AD=AC=2，E為CD的中點，M在AB上，且

  AM

  =

  2

  MB

  ．
  （1）求證：EM∥平面PAD；
  （2）求平面PAD與平面PBC夾角的正弦值；
  （3）點F是線段PD上異于兩端點的任意一點，若滿足異面直線EF與AC所成角為45°，求AF的長．
  組卷：55引用：1難度：0.5

  解析