2022-2023學年四川省廣安市高二（上）期末數學試卷（理科）

一、選擇題：本大題共12個小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知直線l₁：x+y=0與直線l₂：ax-y+8=0平行，則a值為（　　）

  A．2

  B．-1

  C．8

  D．4
  組卷：25引用：2難度：0.7

  解析

• 2．已知 a,b是兩條不同的直線，α，β是兩個不同的平面，則下列說法正確的是（　　）

  A．若a∥α，b∥α，則a∥b	B．若α⊥β，a?α，b?β，則a⊥b
  C．若a⊥b,b⊥α，則a∥α	D．若α∥β，a?α，則a∥β
  組卷：52引用：4難度：0.7

  解析

• 3．已知點A與點B（2，1）關于直線x+y+2=0對稱，則點A的坐標為（　　）

  A．（-1，4）

  B．（4，5）

  C．（-3，-4）

  D．（-4，-3）
  組卷：279引用：4難度：0.7

  解析

• 4．宋元時期，中國數學鼎盛時期中杰出的數學家有“秦〔九韶〕、李〔冶〕、楊〔輝〕、朱〔世杰〕四大家”，朱世杰就是其中之一．他的著作《算學啟蒙》中，記載有這樣一個“松竹并生”的問題：松長四尺，竹長兩尺，松日自半，竹日自倍，松竹何日而長等．如圖是源于其思想的一個程序框圖．若輸入的a,b分別為4，2，則輸出的n=（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：9引用：1難度：0.8

  解析

• 5．關于用統計方法獲取、分析數據，下列結論錯誤的是（　　）

  A．質檢機構為檢測一大型超市某商品的質量情況，合理的調查方式為抽樣調查

  B．若甲、乙兩組數據的標準差滿足S甲＜S乙，則可以估計甲比乙更穩定

  C．若數據x1，x2，x3，?，xn的平均數為 x ，則數據yi=axi-b（i=1，2，3，?，n）的平均數為 a x - b

  D．為了解高一學生的視力情況，現有高一男生200人，女生400人，按性別進行分層抽樣，樣本量按比例分配，若從女生中抽取的樣本量為80，則男生樣本容量為60
  組卷：111引用：7難度：0.8

  解析

• 6．若圓C₁：（x-1）²+y²=1與圓C₂：（x-5）²+（y-3）²=30-m有且僅有3條公切線，則m=（　　）

  A．14

  B．28

  C．9

  D．-11
  組卷：319引用：4難度：0.8

  解析

• 7．若x,y滿足約束條件

  x - y + 2 ≥ 0

  x + y - m ≥ 0

  x - 3 ≤ 0

  ，則z=2x-3y的最大值為9，則正實數m的值為（　　）

  A．1

  B．2

  C．4

  D．8
  組卷：171引用：2難度：0.8

  解析

三、解答題：共70分。解答應寫出文字說明、證明過程或演算步驟。

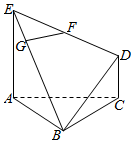• 21．在多面體ABCDE中，平面ACDE⊥平面ABC，四邊形ACDE為直角梯形，CD∥AE，AC⊥AE，AB⊥BC，CD=1，AE=AC=2，F為DE的中點，且點E滿足

  EB

  =

  4

  EG

  ．
  （1）證明：GF∥平面ABC；
  （2）當多面體ABCDE的體積最大時，求二面角A-BE-D的余弦值．
  組卷：567引用：11難度：0.4

  解析

• 22．平面直角坐標系中，已知圓C的半徑為2，圓心在y軸的正半軸上，直線4x+3y+4=0與圓C相切．
  （1）求圓C的方程；
  （2）設D（0，1），過點D作直線l₁，交圓C于P、Q兩點，P、Q不在y軸上，過點D作與直線l₁垂直的直線l₂，交圓C于E、F兩點，記四邊形EPFQ的面積為S，求S的最大值．
  組卷：41引用：2難度：0.6

  解析