2022-2023學(xué)年安徽省安慶外國(guó)語(yǔ)學(xué)校高二（上）第一次月考數(shù)學(xué)試卷

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．已知空間向量

  a

  =（-3，2，5），

  b

  =（1，x,-1），且

  a

  與

  b

  垂直，則x等于（　　）

  A．4

  B．1

  C．3

  D．2
  組卷：141引用：11難度：0.8

  解析

• 2．在下列條件中，一定能使空間中的四點(diǎn)M，A，B，C共面的是（　　）

  A． OM = 2 OA - OB - OC	B． OM = 1 5 OA + 1 3 OB + 1 2 OC
  C． MA + 2 MB + MC = 0	D． OM + OA + OB + OC = 0
  組卷：512引用：11難度：0.7

  解析

• 3．設(shè)點(diǎn)A（4，2，-1），O（0，0，0），M（1，-1，2），若

  OM

  =

  AB

  ，則點(diǎn)B的坐標(biāo)為（　　）

  A．（-1，3，-3）

  B．（1，-3，3）

  C．（5，1，1）

  D．（-5，-1，-1）
  組卷：147引用：1難度：0.8

  解析

• 4．下列說(shuō)法正確的是（　　）

  A．若直線l的方向向量與平面α的法向量的夾角等于150°，則直線l與平面α所成的角等于30°

  B．二面角的大小范圍是[0，π]

  C．兩條異面直線的夾角等于它們的方向向量的夾角

  D．二面角的大小等于其兩個(gè)半平面的法向量的夾角的大小
  組卷：37引用：3難度：0.7

  解析

• 5．已知M（4，3，1），記M到x軸的距離為a,到y(tǒng)軸的距離為b,到z軸的距離為c,則（　　）

  A．a(chǎn)＞b＞c

  B．c＞a＞b

  C．c＞b＞a

  D．b＞c＞a
  組卷：91引用：2難度：0.7

  解析

• 6．若向量

  a

  =

  （

  1

  ，-

  2

  ，

  3

  ）

  ，

  b

  =

  （

  -

  2

  ，

  3

  ，-

  1

  ）

  ，則

  |

  a

  +

  2

  b

  |

  =（　　）

  A． 2 7

  B．5

  C． 26

  D． 4 2
  組卷：966引用：8難度：0.7

  解析

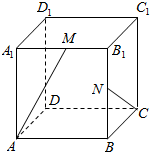• 7．在棱長(zhǎng)為1的正方體ABCD-A₁B₁C₁D₁中，M和N分別為A₁B₁和BB₁的中點(diǎn)，那么直線AM與CN所成角的余弦值是（　　）

  A． 3 2

  B． 10 10

  C． 3 5

  D． 2 5
  組卷：612引用：44難度：0.9

  解析

四、解答題：本大題共6個(gè)大題，共70分，解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟．

• 21．如圖，在正四棱錐P-ABCD中，O為底面中心，PO=AO=3，M為PO的中點(diǎn)，

  PE

  =2

  EB

  ．
  （1）求證：DM∥平面EAC；
  （2）求直線DM到平面EAC的距離．
  組卷：87引用：8難度：0.5

  解析

• 22．在四棱錐P-ABCD中，底面ABCD是邊長(zhǎng)為2的菱形，∠ABC=60°，PA⊥PB，PA=PB，PC=2．
  （Ⅰ）證明：平面PAB⊥平面ABCD；
  （Ⅱ）H為PA的中點(diǎn)，求二面角D-CH-B的余弦值．
  組卷：85引用：5難度：0.4

  解析