2022-2023學年福建省福州市八縣（市）協作校高二（下）期末數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={x∈Z|x²-4≤0}，B={1，2}，則A∪B=（　　）

  A．{0，1，2}	B．{-2，-1，0，1，2}
  C．{-2，-1，1，2}	D．{-1，0，1，2}
  組卷：75引用：2難度：0.8

  解析

• 2．若復數z滿足z?（1+i）=2，則復數z的虛部為（　　）

  A．-i

  B．i

  C．-1

  D．1
  組卷：24引用：1難度：0.8

  解析

• 3．已知sinα+

  2

  cosα=0，則tan2α=（　　）

  A．2 2

  B．-2 2

  C． 2

  D． 2 4
  組卷：190引用：3難度：0.7

  解析

• 4．南宋數學家楊輝所著的《詳解九章算法?商功》中出現了如圖所示的形狀，后人稱之為“三角垛”．“三角垛”的最上層（即第一層）有1個球，第二層有3個球，第三層有6個球，…．若“三角垛”從第一層到第n層的各層的球數構成一個數列{a_n}，則（　　）

  A．a6-a5=5	B．a10=45
  C．an+an+2=2an+1	D．an+1-an=n+1
  組卷：38引用：1難度：0.8

  解析

• 5．已知p：a+b≤6，q：ab≤9，則p是q的（　　）條件．

  A．充分不必要	B．必要不充分
  C．充分必要	D．既不充分也不必要
  組卷：79引用：1難度：0.8

  解析

• 6．已知四邊形ABCD是平行四邊形，

  AE

  =

  2

  EB

  ，若EC與BD交于點O，且

  EO

  =

  λ

  AB

  +

  1

  4

  ED

  ，則λ=（　　）

  A． 1 4

  B． 3 8

  C． 1 2

  D． 3 4
  組卷：66引用：1難度：0.7

  解析

• 7．設點F₁，F₂分別是橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦點，點M，N在C上（M位于第一象限），且點M，N關于原點對稱，若|MN|=|F₁F₂|，|NF₂|=3|MF₂|，則C的離心率為（　　）

  A． 10 8

  B． 10 4

  C． 5 8

  D． 5 5 8
  組卷：188引用：1難度：0.5

  解析

四、解答題：本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

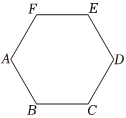• 21．如圖，正六邊形ABCDEF的邊長為4．已知雙曲線Γ的焦點分別為A，D，兩條漸近線分別為直線BE，CF．
  （1）建立適當的平面直角坐標系，求Γ的方程；
  （2）過點A的直線l與Γ交于P，Q兩點，

  AP

  =

  λ

  AQ

  （

  λ

  ≠

  -

  1

  ）

  ，若點M滿足

  PM

  =

  λ

  MQ

  ，證明：點M在一條定直線上．
  組卷：23引用：1難度：0.5

  解析

• 22．已知函數f（x）=ax+

  b

  x

  -lnx,其中a,b∈R．
  （1）若b=0，討論函數f（x）的單調性；
  （2）已知x₁，x₂是函數f（x）的兩個零點，且x₁＜x₂，證明：x₂（ax₁-1）＜b＜x₁（ax₂-1）．
  組卷：49引用：1難度：0.5

  解析