2019-2020學年山東省威海市乳山市六年級（上）期末數學試卷（五四學制）

一、選擇題（本大題共12小題，每小題3分，共36分．在每小題給出的四個選項中，只有一個是正確的．每小題選對得3分，選錯、不選或多選，均不得分）

• 1．-3與它的相反數的和是（　　）

  A．-6

  B．0

  C．3

  D．-3
  組卷：6引用：1難度：0.9

  解析

• 2．城市地鐵運營極大地緩解了城市中心的交通壓力．據統計，某市新增的一條地鐵線每天承運力約為185000人次，數據“185000”用科學記數法表示為（　　）

  A．1.85×105

  B．1.85×104

  C．1.85×106

  D．18.5×105
  組卷：8引用：1難度：0.9

  解析

• 3．若-x³y^a與x^by是同類項，則a+b的值為（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：7171引用：49難度：0.7

  解析

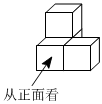• 4．下圖所示的幾何體是由若干個大小相同的小立方塊搭成的，則這個幾何體從左面看到的形狀圖為（　　）

  A．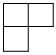

  B．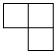

  C．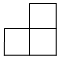

  D．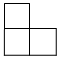
  組卷：14引用：3難度：0.7

  解析

• 5．已知關于x的方程2x+a-5=0的解是x=2，則a的值為（　　）

  A．1

  B．-1

  C．9

  D．-9
  組卷：325引用：4難度：0.7

  解析

• 6．對于“-a”所表示的點，可以借助數軸從“形”的角度理解．下列說法錯誤的是（　　）

  A．該點一定在原點左側

  B．該點與表示的數為a的點到原點的距離一定相等

  C．該點可能在原點右側

  D．該點可能在原點上
  組卷：21引用：1難度：0.7

  解析

• 7．圖1和圖2中的所有小正方形的大小均相同．將圖1的正方形放在圖2中的①，②，③，④某一位置，所組成的圖形不能圍成正方體的位置是（　　）

  A．①

  B．②

  C．③

  D．④
  組卷：22引用：2難度：0.7

  解析

• 8．解方程

  2

  -

  3

  x

  -

  5

  6

  =

  3

  -

  x

  3

  ，去分母后應為（　　）

  A．2-（3x-5）=2（3-x）	B．12-（3x-5）=6（3-x）
  C．12-（3x-5）=2（3-x）	D．12-3x-5=2（3-x）
  組卷：6引用：2難度：0.7

  解析

三、解答題（本大題共7小題，共66分，寫出必要的運算、推理過程）

• 24．小明和小強兩人在學校400米長的環形操場跑道勻速跑步，小明的速度是小強速度的1.5倍．兩人從同一起點，同時朝同一方向出發，4分鐘后小明第一次追上小強．（要求：列方程解決問題）
  （1）求小明和小強兩人跑步的速度；
  （2）如果小明和小強兩人從同一起點，同時背向出發，經過多長時間兩人恰好第三次相遇？
  組卷：135引用：2難度：0.4

  解析

• 25．【資料閱讀】
  史料：如圖①，是我國南宋數學家楊輝1261年所著《詳解九章算法》一書中出現的，稱為“楊輝三角”．據資料記載，此圖是楊輝取自賈憲所著《釋鎖算書》，故也稱“賈憲三角”．歐洲人帕斯卡在1654年也有類似的發現，稱為“帕斯卡三角形”，比楊輝遲393年，比賈憲遲600年．楊輝三角是一種離散型數與形的結合，把組合數內在的一些規律直觀地從圖形中體現了出來，是中國古代數學的杰出研究成果之一．
  規定：若a≠0，則a⁰=1．
  
  【問題探究】
  （1）將“楊輝三角”簡化為圖②，按照規律：
  ①第8行添加的數分別為

  ；（相鄰兩數之間要用“，”分隔開）
  ②第100行的數之和用冪可以表示為

  ．
  （2）如圖③，分別畫出7條斜線，并計算出了每條斜線經過的數之和．若繼續畫出第10條斜線，該直線經過的數之和為

  ．
  
  【拓展延伸】
  （3）結合“問題探究”中問題（2）揭示的規律，作如下正方形（數字即為正方形的邊長）：
  
  利用上面的正方形按一定規律建構如下長方形，并依次記為長方形（1），長方形（2），長方形（3），長方形（4）．
  
  按照這樣的規律繼續建構長方形，則長方形（11）的周長為

  ．
  組卷：179引用：1難度：0.1

  解析