2020-2021學(xué)年北京二中高一（下）第六學(xué)段數(shù)學(xué)試卷

一、選擇題（共12小題，每小題4分，共48分.選出符合題目要求的一項(xiàng)）

• 1．設(shè)復(fù)數(shù)z=1+2i（i為虛數(shù)單位），則在復(fù)平面內(nèi)z對(duì)應(yīng)的點(diǎn)位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：41引用：2難度：0.9

  解析

• 2．已知向量

  a

  ，

  b

  不共線，

  c

  =k

  a

  +

  b

  ，

  d

  =

  a

  -

  b

  ，如果

  c

  ∥

  d

  ，那么（　　）

  A．k=1且 c 與 d 同向	B．k=1且 c 與 d 反向
  C．k=-1且 c 與 d 同向	D．k=-1且 c 與 d 反向
  組卷：67引用：2難度：0.9

  解析

• 3．已知圓C：x²+y²-2x-my=0上任意一點(diǎn)M關(guān)于直線y=x的對(duì)稱點(diǎn)N也在圓上．則m的值為（　　）

  A．1

  B．2

  C．-1

  D．-2
  組卷：15引用：1難度：0.8

  解析

• 4．在△ABC中，∠A，∠B，∠C所對(duì)的邊長(zhǎng)分別為a,b,c,如果acosB=bcosA，那么△ABC一定是（　　）

  A．銳角三角形

  B．鈍角三角形

  C．直角三角形

  D．等腰三角形
  組卷：78引用：9難度：0.9

  解析

• 5．當(dāng)點(diǎn)P在圓x²+y²=1上變動(dòng)時(shí)，它與定點(diǎn)Q（-3，0）的連結(jié)線段PQ的中點(diǎn)的軌跡方程是（　　）

  A．（x+3）2+y2=4	B．（x-3）2+y2=4
  C．（2x-3）2+4y2=1	D．（2x+3）2+4y2=1
  組卷：332引用：15難度：0.7

  解析

• 6．復(fù)數(shù)z滿足（z-3）（2-i）=5（i為虛數(shù)單位），則z的共軛復(fù)數(shù)

  z

  為（　　）

  A．2+i

  B．2-i

  C．5+i

  D．5-i
  組卷：803引用：37難度：0.9

  解析

• 7．已知a,b是兩條不重合的直線，α，β是兩個(gè)不重合的平面，下列命題中正確的是（　　）

  A．a(chǎn)∥b,b∥α，則a∥α

  B．a(chǎn),b?α，a∥β，b∥β，則α∥β

  C．a(chǎn)⊥α，b∥α，則a⊥b

  D．當(dāng)a?α，且b?α?xí)r，若b∥α，則a∥b
  組卷：52引用：14難度：0.9

  解析

• 8．設(shè)a∈R，則“a=-2”是直線l₁：ax+2y-1=0與直線l₂：x+（a+1）y-1=0平行的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：147引用：4難度：0.8

  解析

三、解答題（共5小題，共67分.解答應(yīng)寫(xiě)出文字說(shuō)明，演算步驟或證明過(guò)程）

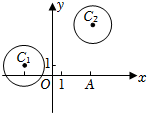• 23．如圖，在平面直角坐標(biāo)系xOy中，已知圓C₁：（x+3）²+（y-1）²=4和圓C₂：（x-4）²+（y-5）²=4．
  （1）若直線l過(guò)點(diǎn)A（4，0），且被圓C₁截得的弦長(zhǎng)為

  2

  3

  ，求直線l的方程；
  （2）設(shè)P為平面上的點(diǎn)，滿足：存在過(guò)點(diǎn)P的無(wú)窮多對(duì)互相垂直的直線l₁和l₂，它們分別與圓C₁和圓C₂相交，且直線l₁被圓C₁截得的弦長(zhǎng)與直線l₂被圓C₂截得的弦長(zhǎng)相等，試求所有滿足條件的點(diǎn)P的坐標(biāo)．
  組卷：278引用：11難度：0.6

  解析

• 24．已知集合M={1，2，3，?，n}（n∈N^*），若集合

  A

  =

  {

  a

  1

  ，

  a

  2

  ，

  ?

  ，

  a

  m

  }

  ?

  M

  （

  m

  ∈

  N

  *

  ）

  ．且對(duì)任意的b∈M，存在a_i，a_j∈A（1≤i≤j≤m），使得b=λ₁a_i+λ₂a_j其中λ₁，λ₂∈{-1，0，1}，則稱集合A為集合M的一個(gè)m元基底．
  （1）分別判斷下列集合A是否為集合M的一個(gè)二元基底，并說(shuō)明理由；
  ①A={1，5}，M={1，2，3，4，5}；②A={2，3}，M={1，2，3，4，5，6}．
  （2）若集合A是集合M的一個(gè)m元基底，證明：m（m+1）≥n；
  （3）若集合A為集合M={1，2，3，?，19}的一個(gè)m元基底，求出m的最小可能值，并求出當(dāng)m取最小值時(shí)M的一個(gè)基底A．
  組卷：107引用：4難度：0.2

  解析