2021-2022學年陜西省銅川一中高二（下）期末數學試卷（文科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

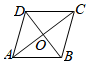• 1．如圖，在四邊形ABCD中，AC與BD交于點O，若

  AD

  =

  BC

  ，則下面互為相反向量的是（　　）

  A． AC 與 CB

  B． OB 與 OD

  C． AB 與 DC

  D． AO 與 OC
  組卷：324引用：3難度：0.9

  解析

• 2．已知角α的終邊經過點P（4，-3），則sinα+cosα的值是（　　）

  A． 1 5

  B． - 1 5

  C． 7 5

  D． - 7 5
  組卷：505引用：11難度：0.9

  解析

• 3．在△ABC中，若A=120°，

  AB

  =

  7

  ，

  BC

  =

  21

  ，則AC=（　　）

  A． 7

  B． 14

  C． 21

  D． 2 7
  組卷：191引用：1難度：0.7

  解析

• 4．已知扇形的圓心角為120°，面積為

  4

  π

  3

  ，則該扇形所在圓的半徑為（　　）

  A．1

  B．2

  C． 3

  D． 2
  組卷：429引用：2難度：0.8

  解析

• 5．在△ABC中，角A，B，C所對的邊分別為a,b,c,若

  b

  =

  33

  ，

  c

  =

  11

  ，B=60°，則C=（　　）

  A．30°

  B．60°

  C．150°

  D．30°或150°
  組卷：232引用：1難度：0.8

  解析

• 6．把函數

  y

  =

  sin

  （

  2

  x

  -

  π

  6

  ）

  的圖像上所有的點向左平移

  π

  24

  個單位長度，再把所得圖像上所有點的橫坐標縮短為原來的

  1

  2

  （縱坐標不變），得到的圖像所對應的函數解析式是（　　）

  A． y = sin （ x - 5 π 24 ）	B． y = sin （ 4 x - π 4 ）
  C． y = sin （ x - π 8 ）	D． y = sin （ 4 x - π 12 ）
  組卷：191引用：2難度：0.7

  解析

• 7．已知

  sinθ

  =

  2

  sin

  （

  3

  π

  2

  -

  θ

  ）

  ，則sin2θ+cos²θ=（　　）

  A． - 2 5

  B． 2 5

  C． - 3 5

  D． 3 5
  組卷：74引用：2難度：0.7

  解析

三、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數

  f

  （

  x

  ）

  =

  cos

  （

  2

  x

  -

  π

  3

  ）

  -

  2

  co

  s

  2

  x

  +

  1

  ．
  （1）求函數f（x）的單調遞增區間；
  （2）求函數f（x）在區間

  [

  -

  π

  12

  ，

  π

  2

  ]

  上的值域．
  組卷：111引用：1難度：0.7

  解析

• 22．在△ABC中，a,b,c分別為內角A，B，C的對邊，△ABC的面積

  S

  =

  1

  4

  c

  2

  ．
  （1）若

  2

  ccos

  B

  =

  2

  a

  -

  b

  ，求

  sin

  A

  sin

  B

  的值；
  （2）求

  a

  b

  的取值范圍．
  組卷：1056引用：8難度：0.5

  解析