2023年湖北省孝感市安陸市、云夢(mèng)縣、孝昌縣、大悟縣中考數(shù)學(xué)二模試卷

一、精心選一選（本大題共8小題，每小題3分，滿(mǎn)分24分，在每小題給出的四個(gè)選項(xiàng)中只有一項(xiàng)是符合題目要求的，請(qǐng)?jiān)诖痤}卡上把正確答案的代號(hào)涂黑）

• 1．-2的相反數(shù)是（　　）

  A．2

  B．-2

  C． 1 2

  D． - 1 2
  組卷：1200引用：63難度：0.9

  解析

• 2．如圖是某幾何體的三視圖，則該幾何體是（　　）

  A．圓錐

  B．圓柱

  C．正三棱柱

  D．正三棱錐
  組卷：83引用：5難度：0.9

  解析

• 3．ChatGPT是人工智能研究實(shí)驗(yàn)室OpenAI新推出的一種人工智能技術(shù)驅(qū)動(dòng)的自然語(yǔ)言處理工具，ChatGPT的背后離不開(kāi)大模型、大數(shù)據(jù)、大算力，其技術(shù)底座有著多達(dá)1750億個(gè)模型參數(shù)，數(shù)字1750用科學(xué)記數(shù)法表示為（　　）

  A．1.75×102

  B．1.75×103

  C．0.175×103

  D．0.175×104
  組卷：68引用：3難度：0.5

  解析

• 4．下列新能源汽車(chē)標(biāo)志圖案中，既是軸對(duì)稱(chēng)圖形又是中心對(duì)稱(chēng)圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：343引用：19難度：0.7

  解析

• 5．下列運(yùn)算正確的是（　　）

  A．a(chǎn)2+2a2=3a4	B．（-2a3）2=-4a6
  C．a(chǎn)2?a4=a8	D．a(chǎn)6÷a3=a3
  組卷：22引用：1難度：0.7

  解析

• 6．九年級(jí)某班準(zhǔn)備從班上19名女生中，挑選10名身高較高的同學(xué)參加校排球比賽，若這19名女生的身高各不相同，其中女生小紅想知道自己能否入選，只需知道這19名女生身高數(shù)據(jù)的（　　）

  A．中位數(shù)

  B．平均數(shù)

  C．最小值

  D．方差
  組卷：62引用：1難度：0.5

  解析

• 7．如圖，分別以△ABC的三個(gè)頂點(diǎn)為圓心，作半徑均為1的三個(gè)圓，三圓兩兩不相交，那么三個(gè)圓落在△ABC內(nèi)的三段弧長(zhǎng)度之和為（　　）

  A．3π

  B．2π

  C．π

  D． 1 2 π
  組卷：273引用：1難度：0.5

  解析

• 8．拋物線(xiàn)y=ax²+bx+c （a,b,c為常數(shù)，且a≠0）開(kāi)口向下且過(guò)點(diǎn)A（1，0），B（m,0），其中-2＜m＜-1，下列結(jié)論：①abc＞0；②a-b+c＞0；③a（m+1）-b+c＞0；④若方程a（x-m）（x-1）-1=0有兩個(gè)不相等的實(shí)數(shù)根，則4ac-b²＞4a,其中結(jié)論正確的個(gè)數(shù)是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：104引用：2難度：0.6

  解析

三、專(zhuān)心解一解（本大題共8小題，滿(mǎn)分72分，請(qǐng)認(rèn)真讀題，冷靜思考，解答題應(yīng)寫(xiě)出必要的文字說(shuō)明、證明過(guò)程或演算步驟，請(qǐng)把解題過(guò)程寫(xiě)在答題卡相應(yīng)題號(hào)的位置）

• 23．（1）（問(wèn)題提出）如圖1，在Rt△ABC中，AB=AC，∠BAC=90°，D為BC的中點(diǎn)，E，F(xiàn)分別是線(xiàn)段AB，AC上的點(diǎn)，且∠EDF=90°，判斷線(xiàn)段DE與DF的數(shù)量關(guān)系，并說(shuō)明理由；
  （2）（類(lèi)比探究）如圖2，若

  AB

  =

  1

  2

  AC

  ，其他條件不變，（1）中的結(jié)論是否仍然成立？若成立，請(qǐng)說(shuō)明理由；若不成立，請(qǐng)寫(xiě)出此時(shí)線(xiàn)段DE與DF的數(shù)量關(guān)系，并給予證明；
  （3）（拓展應(yīng)用）如圖3，在Rt△ABC中，∠BAC=90°，D為BC的中點(diǎn)，F(xiàn)在線(xiàn)段AB上，E在AB的延長(zhǎng)線(xiàn)上，且∠EDF=90°，若

  AB

  =

  1

  2

  AC

  ，

  AF

  =

  1

  3

  FB

  ，求

  FB

  BE

  的值．
  
  組卷：148引用：1難度：0.2

  解析

• 24．已知拋物線(xiàn)y=ax²+bx+4過(guò)A（-1，0），B（4，0）兩點(diǎn)，交y軸于點(diǎn)C．
  （1）求拋物線(xiàn)的解析式及其對(duì)稱(chēng)軸；
  （2）如圖1，若點(diǎn)P是線(xiàn)段OC上的一動(dòng)點(diǎn)，連接AP、BP，將△ABP沿直線(xiàn)BP翻折，得到△A′BP，當(dāng)點(diǎn)A′恰好落在該拋物線(xiàn)的對(duì)稱(chēng)軸上時(shí)，求點(diǎn)P的坐標(biāo)；
  （3）如圖2，與直線(xiàn)BC垂直的直線(xiàn)y=x+t與拋物線(xiàn)在第一象限交于點(diǎn)M，與線(xiàn)段BC、線(xiàn)段AC分別交于點(diǎn)N和點(diǎn)E，過(guò)點(diǎn)E作EH⊥x軸于點(diǎn)H，求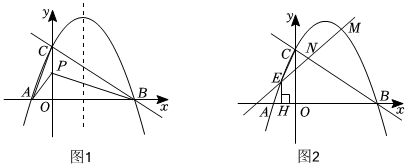

  EH

  +

  2

  EM

  的最大值．
  
  組卷：88引用：1難度：0.3

  解析