湘教新版九年級（下）中考題單元試卷：第1章 二次函數（08）

一、選擇題（共18小題）

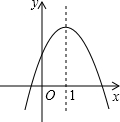• 1．二次函數y=-x²+bx+c的圖象如圖所示：若點A（x₁，y₁），B（x₂，y₂）在此函數圖象上，x₁＜x₂＜1，y₁與y₂的大小關系是（　　）

  A．y1≤y2

  B．y1＜y2

  C．y1≥y2

  D．y1＞y2
  組卷：1336引用：77難度：0.9

  解析

• 2．如果一種變換是將拋物線向右平移2個單位或向上平移1個單位，我們把這種變換稱為拋物線的簡單變換．已知拋物線經過兩次簡單變換后的一條拋物線是y=x²+1，則原拋物線的解析式不可能的是（　　）

  A．y=x2-1

  B．y=x2+6x+5

  C．y=x2+4x+4

  D．y=x2+8x+17
  組卷：2933引用：73難度：0.9

  解析

• 3．要將拋物線y=x²+2x+3平移后得到拋物線y=x²，下列平移方法正確的是（　　）

  A．向左平移1個單位，再向上平移2個單位

  B．向左平移1個單位，再向下平移2個單位

  C．向右平移1個單位，再向上平移2個單位

  D．向右平移1個單位，再向下平移2個單位
  組卷：5385引用：87難度：0.9

  解析

• 4．將拋物線y=x²向右平移2個單位，再向上平移3個單位后，拋物線的解析式為（　　）

  A．y=（x+2）2+3

  B．y=（x-2）2+3

  C．y=（x+2）2-3

  D．y=（x-2）2-3
  組卷：2462引用：88難度：0.9

  解析

• 5．將拋物線y=x²-2x+3向上平移2個單位長度，再向右平移3個單位長度后，得到的拋物線的解析式為（　　）

  A．y=（x-1）2+4

  B．y=（x-4）2+4

  C．y=（x+2）2+6

  D．y=（x-4）2+6
  組卷：5249引用：106難度：0.9

  解析

• 6．拋物線y=3x²+2x-1向上平移4個單位長度后的函數解析式為（　　）

  A．y=3x2+2x-5

  B．y=3x2+2x-4

  C．y=3x2+2x+3

  D．y=3x2+2x+4
  組卷：1065引用：62難度：0.9

  解析

• 7．將拋物線y=-2x²+1向右平移1個單位長度，再向上平移1個單位長度所得的拋物線解析式為（　　）

  A．y=-2（x+1）2	B．y=-2（x+1）2+2
  C．y=-2（x-1）2+2	D．y=-2（x-1）2+1
  組卷：1472引用：65難度：0.9

  解析

• 8．將拋物線y=x²向左平移2個單位長度，再向下平移3個單位長度，得到的拋物線的函數表達式為（　　）

  A．y=（x+2）2-3

  B．y=（x+2）2+3

  C．y=（x-2）2+3

  D．y=（x-2）2-3
  組卷：2011引用：99難度：0.9

  解析

• 9．把拋物線y=-2x²先向右平移1個單位長度，再向上平移2個單位長度后，所得函數的表達式為（　　）

  A．y=-2（x+1）2+2	B．y=-2（x+1）2-2
  C．y=-2（x-1）2+2	D．y=-2（x-1）2-2
  組卷：1435引用：98難度：0.9

  解析

• 10．如果將拋物線y=x²向右平移1個單位，那么所得的拋物線的表達式是（　　）

  A．y=x2-1

  B．y=x2+1

  C．y=（x-1）2

  D．y=（x+1）2
  組卷：685引用：61難度：0.9

  解析

三、解答題（共2小題）

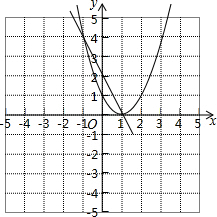• 29．設函數y=（x-1）[（k-1）x+（k-3）]（k是常數）．
  （1）當k取1和2時的函數y₁和y₂的圖象如圖所示，請你在同一平面直角坐標系中畫出當k取0時的函數的圖象；
  （2）根據圖象，寫出你發現的一條結論；
  （3）將函數y₂的圖象向左平移4個單位，再向下平移2個單位，得到的函數y₃的圖象，求函數y₃的最小值．
  組卷：2920引用：55難度：0.5

  解析

• 30．已知拋物線y=a（x-3）²+2經過點（1，-2）．
  （1）求a的值；
  （2）若點A（m,y₁）、B（n,y₂）（m＜n＜3）都在該拋物線上，試比較y₁與y₂的大小．
  組卷：1871引用：64難度：0.5

  解析