2022-2023學年福建省廈門市雙十中學高三(上)期中數學試卷
發布:2024/10/30 21:0:2
一、單選題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知全集U=R,集合A={0,1,2},B={x|x2+x=0},則下列關于集合A,B關系的韋恩圖正確的是( )
A. 
B. 
C. 
D.  組卷:85引用:2難度:0.7
組卷:85引用:2難度:0.7 -
2.已知復數z=
,則z的共軛復數-i3+i=zA. -1-3i4B. -1-3i2C. -1+3i4D. -1+3i2組卷:39引用:3難度:0.7 -
3.已知a,b∈R,ab≠0,則使
<1a成立的一個充分不必要條件是( )1bA.a>b B.a<b<0 C.ab(a-b)>0 D.a>b>0 組卷:42引用:2難度:0.7 -
4.將y=sin(3x-
)圖象上每一個點的橫坐標變為原來的3倍(縱坐標不變),得到y=g(x)的圖象,再將y=g(x)圖象向左平移3π4,得到y=φ(x)的圖象,則y=φ(x)的解析式為( )3π4A.y=sinx B.y=cosx C.y=sin9x D.y=sin(9x- )3π2組卷:545引用:3難度:0.8 -
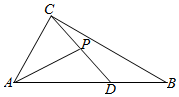 5.如圖,在△ABC中,∠BAC=,π3,P為CD上一點,且滿足AD=2DB=mAP+AC,若|12AB|=2,|AC|=3,則|AB|的值為( )AP
5.如圖,在△ABC中,∠BAC=,π3,P為CD上一點,且滿足AD=2DB=mAP+AC,若|12AB|=2,|AC|=3,則|AB|的值為( )APA. 13B. 132C. 133D. 134組卷:209引用:5難度:0.7 -
6.已知α∈(0,π),且3cos2α-8cosα=5,則sin2α=( )
A. -49B. -459C. -4527D. 52組卷:202引用:1難度:0.7 -
7.納皮爾是蘇格蘭數學家,其主要成果有球面三角中的納皮爾比擬式,納皮爾圓部法則(1614)和納皮爾算籌(1617),而最大的貢獻是對數的發明,著有《奇妙的對數定律說明書》,并且發明了對數表,可以利用對數表查詢出任意對數值.現將物體放在空氣中冷卻,如果物體原來的溫度是T1(℃),空氣的溫度是T0(℃),經過l分鐘后物體的溫度T(℃)可由公式t=4[log3(T1-T0)-log3(T-T0)]得出;現有一杯溫度為70℃的溫水,放在空氣溫度為零下10℃的冷藏室中,則當水溫下降到10℃時,經過的時間約為( )
參考數據:lg2≈0.301,lg3≈0.477.A.3.048分鐘 B.4.048分鐘 C.5.048分鐘 D.6.048分鐘 組卷:112引用:7難度:0.8
四、解答題:本題共6小題,共70分.解答應寫出文字說明,證明過程或演算步驟.
-
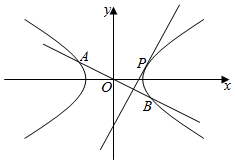 21.在平面直角坐標系xOy中,已知雙曲線C:x2a2=1(a>0,b>0)的右焦點為(3,0),且經過點(2-y2b2,1).2
21.在平面直角坐標系xOy中,已知雙曲線C:x2a2=1(a>0,b>0)的右焦點為(3,0),且經過點(2-y2b2,1).2
(1)求雙曲線C的標準方程;
(2)已知A,B是雙曲線C上關于原點對稱的兩點,垂直于AB的直線l與雙曲線C有且僅有一個公共點P,當點P位于第一象限,且△PAB被x軸分割為面積比為3:2的兩部分時,求直線AB的方程.組卷:181引用:6難度:0.4 -
22.已知函數f(x)=
(a∈R).a+lnxx
(1)當函數f(x)與函數g(x)=lnx圖象的公切線1經過坐標原點時,求實數a的值;
(2)證明:當a∈(0,)時,函數h(x)=f(x)-ax有兩個零點x1,x2,且滿足12+1x1<1x2.1a組卷:296引用:3難度:0.1


