2020-2021學年陜西省延安市子長中學高二(下)期中數學試卷(文科)
發布:2024/7/6 8:0:9
一、選擇題(本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的)
-
1.設i是虛數單位,且復數z=(1-ai)(3+2i)的實部與虛部互為相反數,其中a為實數,則a=( )
A.5 B.-5 C.3 D.-3 組卷:18引用:3難度:0.8 -
2.下列關于函數、函數的定義域、函數的值域、函數的對應法則的結構圖正確的是( )
A. 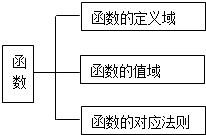
B. 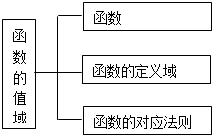
C. 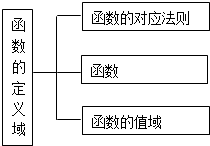
D. 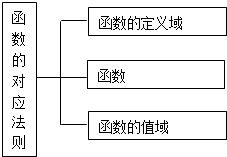 組卷:42引用:10難度:0.9
組卷:42引用:10難度:0.9 -
3.在建立兩個變量y與x的回歸模型中,分別選擇了4個不同的模型,模型1的相關指數R2為0.88,模型2的相關指數R2為0.945,模型3的相關指數R2為0.66,模型4的相關指數R2為0.01,其中擬合效果最好的模型是( )
A.模型1 B.模型2 C.模型3 D.模型4 組卷:345引用:3難度:0.9 -
4.下列關于函數f(x)=1+x-sinx的說法正確的是( )
A.增函數 B.減函數 C.在(0,π)上單調遞增,在(π,2π)上單調遞減 D.在(0,π)上單調遞減,在(π,2π)上單調遞增 組卷:6引用:2難度:0.8 -
5.下列各對事件中,不互為相互獨立事件的是( )
A.甲、乙兩運動員各射擊一次,事件M“甲射中10環”,事件N“乙射中9環” B.甲組3名男生,2名女生;乙組2名男生,3名女生,現從甲、乙兩組中各選1名學生參加演講比賽,事件M“從甲組中選出1名男生”,事件N“從乙組中選出1名女生” C.袋中有3白、2黑共5個大小相同的小球,依次有放回地摸兩球,事件M“第一次摸到白球”,事件N“第二次摸到白球” D.袋中有3白、2黑共5個大小相同的小球,依次不放回地摸兩球,事件M“第一次摸到白球”,事件N“第二次摸到黑球” 組卷:16引用:4難度:0.7 -
6.若a,b,c是不全相等的實數,求證:a2+b2+c2>ab+bc+ca.證明過程如下:
因為a,b,c∈R,所以a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac.又因為a,b,c不全相等,所以以上三式至少有一個等號不成立,所以以上三式相加得2(a2+b2+c2)>2(ab+bc+ac).
所以a2+b2+c2>ab+bc+ca.此證法是( )A.分析法 B.綜合法 C.分析法與綜合法并用 D.反證法 組卷:83引用:4難度:0.9 -
7.執行如圖所示的程序框圖,則輸出的n=( )
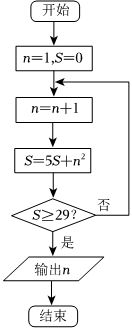
A.2 B.3 C.4 D.5 組卷:133引用:4難度:0.7
三、解答題(本大題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟)
-
21.針對偏遠地區因交通不便、消息閉塞導致優質農產品藏在山中無人識的現象,各地區開始嘗試將電商扶貧作為精準扶貧的重要措施.為了解電商扶貧的效果,某部門隨機就100個貧困地區進行了調查,其當年的電商扶貧年度總投入(單位:萬元)及當年人均可支配年收入(單位:萬元)的貧困地區數目的數據如表:
(1)估計該年度內貧困地區人均可支配年收入過萬的概率;人均可支配年收入(萬元)
電商扶貧年度總投入(萬元)(0.5,1] (1,1.5] (1.5,2] (0,500] 5 3 2 (500,1000] 3 21 6 (1000,3000) 2 34 24
(2)根據所給數據完成下面的列聯表;
(3)根據(2)中的列聯表,判斷能否有99%的把握認為當地的人均可支配年收入是否過萬與當地電商扶貧年度總投入是否超過1千萬有關.人均可支配年收入不超過1萬元 人均可支配年收入超過1萬元 總計 電商扶貧年度總投入不超過1000萬元 電商扶貧年度總投入超過1000萬元 總計
附:,其中n=a+b+c+d.K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)P(K2≥k0) 0.050 0.01 0.005 k0 3.841 6.635 7.879 組卷:2引用:3難度:0.7 -
22.已知函數
在點(-1,f(-1))的切線方程為x+y+3=0.f(x)=ax+bx2+1
(Ⅰ)求函數f(x)的解析式;
(Ⅱ)設g(x)=lnx,求證:g(x)≥f(x)在x∈[1,+∞)上恒成立.組卷:51引用:9難度:0.3


