2023-2024學年四川省成都市錦江區(qū)田家炳中學高三（上）第一次月考數學試卷（理科）

一、單項選擇題：本題共12小題，每小題5分，共60分．

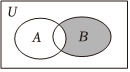• 1．已知全集U=R，集合A={x|x＞3}，B={x|2＜x＜4}，則圖中陰影部分表示的集合為（　　）

  A．[-2，3]

  B．（-2，3）

  C．（2，3]

  D．[-2，3）
  組卷：146引用：5難度：0.9

  解析

• 2．若復數z滿足zi=4-3i,則|z|=（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：20引用：4難度：0.8

  解析

• 3．已知x₁，x₂，…，x_n的平均數為10，標準差為2，則2x₁-1，2x₂-1，…，2x_n-1的平均數和標準差分別為（　　）

  A．19和2

  B．19和3

  C．19和4

  D．19和8
  組卷：318引用：11難度：0.9

  解析

• 4．甲、乙兩名游客慕名來到四川旅游，準備分別從九寨溝、峨眉山、海螺溝、都江堰、青城山這5個景點中隨機選一個．事件A：甲和乙選擇的景點不同，事件B：甲和乙恰好有一人選擇九寨溝．則條件概率P（B|A）=（　　）

  A． 2 5

  B． 3 5

  C． 4 5

  D． 8 25
  組卷：145引用：3難度：0.7

  解析

• 5．已知某三棱錐的三視圖如圖所示，則該三棱錐的體積是（　　）

  A．1

  B． 3 2

  C．3

  D． 9 2
  組卷：210引用：4難度：0.7

  解析

• 6．下列說法中正確的是（　　）
  ①設隨機變量X服從二項分布

  B

  （

  6

  ，

  1

  2

  ）

  ，則

  P

  （

  X

  =

  3

  ）

  =

  5

  16

  
  ②已知隨機變量X服從正態(tài)分布N（2，σ²）且P（X＜4）=0.9，則P（0＜X＜2）=0.4
  ③2023年7月28日第31屆成都大學生運動會在成都隆重開幕，將5名大運會志愿者分配到游泳、乒乓球、籃球和排球4個項目進行志愿者服務，每名志愿者只分配到1個項目，每個項目至少分配1名志愿者，則不同的分配方案共有180種；
  ④E（2X+3）=2E（X）+3，D（2X+3）=4D（X）．

  A．②③

  B．②③④

  C．①②④

  D．①②
  組卷：93引用：2難度：0.6

  解析

• 7．垃圾分類是指按一定規(guī)定或標準將垃圾分類儲存、投放和搬運，從而轉變成公共資源的一系列活動，做好垃圾分類是每一位公民應盡的義務．已知某種垃圾的分解率v與時間t（月）近似地滿足關系v=a?b^t（其中a,b為正常數），經過5個月，這種垃圾的分解率為5%，經過10個月，這種垃圾的分解率為10%，那么這種垃圾完全分解大約需要經過（　　）個月．（參考數據：lg2≈0.3）

  A．20

  B．27

  C．32

  D．40
  組卷：125引用：12難度：0.7

  解析

三、解答題（本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟）

• 21．已知e是自然對數的底數，函數f（x）=

  x

  2

  e

  x

  與F（x）=f（x）-x+

  1

  x

  的定義域都是（0，+∞）．
  （1）求函數f（x）在點（1，f（1））處的切線方程；
  （2）判斷函數F（x）零點個數
  （3）用min{m,n}表示m,n的最小值，設x＞0，g（x）=min{f（x），x-

  1

  x

  }，若函數h（x）=g（x）-cx²在（0，+∞）上為增函數，求實數c的取值范圍．
  組卷：86引用：3難度：0.3

  解析

• 22．在直角坐標系xOy中，曲線C的參數方程為

  x = t + 1 t

  y = t + 1 t

  （t為參數），以坐標原點為極點，x軸正半軸為極軸建立極坐標系，已知直線l的極坐標方程為θ=

  π

  2

  ．
  （1）寫出C的普通方程；
  （2）寫出直線l的直角坐標方程并判斷l(xiāng)與C有無交點，如果有，則求出交點的直角坐標；如果沒有，寫出證明過程．
  組卷：58引用：4難度：0.5

  解析