蘇教版必修2高考題同步試卷：3.1.6 柱、錐、臺、球的體積（01）

一、選擇題（共12小題）

• 1．《九章算術》是我國古代內容極為豐富的數學名著，書中有如下問題：“今有委米依垣內角，下周八尺，高五尺．問：積及為米幾何？”其意思為：“在屋內墻角處堆放米（如圖，米堆為一個圓錐的四分之一），米堆底部的弧長為8尺，米堆的高為5尺，問米堆的體積和堆放的米各為多少？”已知1斛米的體積約為1.62立方尺，圓周率約為3，估算出堆放的米約有（　　）

  A．14斛

  B．22斛

  C．36斛

  D．66斛
  組卷：5131引用：74難度：0.9

  解析

• 2．已知等腰直角三角形的直角邊的長為2，將該三角形繞其斜邊所在的直線旋轉一周而形成的曲面所圍成的幾何體的體積為（　　）

  A． 2 2 π 3

  B． 4 2 π 3

  C．2 2 π

  D．4 2 π
  組卷：3500引用：38難度：0.9

  解析

• 3．在梯形ABCD中，∠ABC=

  π

  2

  ，AD∥BC，BC=2AD=2AB=2，將梯形ABCD繞AD所在的直線旋轉一周而形成的曲面所圍成的幾何體的體積為（　　）

  A． 2 π 3

  B． 4 π 3

  C． 5 π 3

  D．2π
  組卷：2655引用：45難度：0.9

  解析

• 4．已知A，B是球O的球面上兩點，∠AOB=90°，C為該球面上的動點，若三棱錐O-ABC體積的最大值為36，則球O的表面積為（　　）

  A．36π

  B．64π

  C．144π

  D．256π
  組卷：11042引用：72難度：0.9

  解析

• 5．正三棱柱ABC-A₁B₁C₁的底面邊長為2，側棱長為

  3

  ，D為BC中點，則三棱錐A-B₁DC₁的體積為（　　）

  A．3

  B． 3 2

  C．1

  D． 3 2
  組卷：4484引用：61難度：0.9

  解析

• 6．過長方體的一個頂點的三條棱的長分別為3，4，5，且它的八個頂點都在同一個球面上，這球的表面積是（　　）

  A．20 2 π

  B．25 2 π

  C．50π

  D．200π
  組卷：5359引用：65難度：0.9

  解析

• 7．一個四棱錐的側棱長都相等，底面是正方形，其正（主）視圖如圖所示該四棱錐側面積和體積分別是（　　）
  

  A．4 5 ，8

  B． 4 5 ， 8 3

  C． 4 （ 5 + 1 ） ， 8 3

  D．8，8
  組卷：928引用：37難度：0.9

  解析

• 8．某四棱臺的三視圖如圖所示，則該四棱臺的體積是（　　）
  

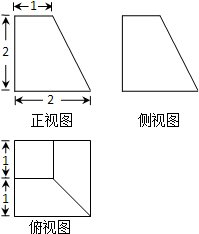
  A．4

  B． 14 3

  C． 16 3

  D．6
  組卷：1031引用：35難度：0.7

  解析

• 9．已知在半徑為2的球面上有A、B、C、D四點，若AB=CD=2，則四面體ABCD的體積的最大值為（　　）

  A． 2 3 3

  B． 4 3 3

  C． 2 3

  D． 8 3 3
  組卷：3128引用：37難度：0.5

  解析

• 10．已知正四棱錐S-ABCD中，SA=2

  3

  ，那么當該棱錐的體積最大時，它的高為（　　）

  A．1

  B． 3

  C．2

  D．3
  組卷：3751引用：47難度：0.7

  解析

三、解答題（共10小題）

• 29．如圖，△ABC和△BCD所在平面互相垂直，且AB=BC=BD=2．∠ABC=∠DBC=120°，E、F、G分別為AC、DC、AD的中點．
  （Ⅰ）求證：EF⊥平面BCG；
  （Ⅱ）求三棱錐D-BCG的體積．
  附：錐體的體積公式V=

  1

  3

  Sh,其中S為底面面積，h為高．
  組卷：2274引用：27難度：0.5

  解析

• 30．如圖，四棱錐P-ABCD中，底面是以O為中心的菱形，PO⊥底面ABCD，AB=2，∠BAD=

  π

  3

  ，M為BC上一點，且BM=

  1

  2

  ．
  （Ⅰ）證明：BC⊥平面POM；
  （Ⅱ）若MP⊥AP，求四棱錐P-ABMO的體積．
  組卷：2952引用：27難度：0.3

  解析