當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省廣州市西關外國語中學高二（上）期末數學試卷

發布：2024/4/20 14:35:0

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知數列{a_n}滿足a₁=1，a_n+1=a_n+3n,則a₆=（　　）
A．30 B．31 C．45 D．46
組卷：508引用：5難度：0.6
解析
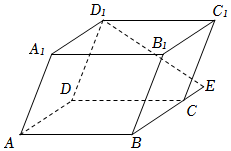2．如圖在平行六面體（底面為平行四邊形的四棱柱）ABCD-A₁B₁C₁D₁中，E為BC延長線上的一點，
BC
=3
CE
，則
D
1
E
=（　　）
A．
AB
+
1
3
AD
-
A
A
1
B．
AB
+
AD
-
2
3
A
A
1
C．
AB
+
1
3
AD
+
A
A
1
D．
AB
-
AD
+
1
3
A
A
1
組卷：113引用：5難度：0.7
解析
3．已知
a
=（2，1，-3），
b
=（-1，2，3），
c
（7，6，λ），若
a
，
b
，
c
三向量共面，則λ=（　　）
A．9 B．-9 C．-3 D．3
組卷：147引用：5難度：0.9
解析
4．已知雙曲線
x
2
a
2
-
y
2
3
=
1
（
a
＞
0
）
的右頂點和拋物線y²=8x的焦點重合，則a的值為（　　）
A．1 B．2 C．3 D．4
組卷：306引用：6難度：0.8
解析
5．已知圓C₁：（x+1）²+y²=25，圓C₂：（x-1）²+y²=1，動圓M與圓C₂外切，同時與圓C₁內切，則動圓圓心M的軌跡方程為（　　）
A．
x
2
3
+
y
2
=
1
B．
x
2
3
+
y
2
2
=
1
C．
x
2
9
+
y
2
=
1
D．
x
2
9
+
y
2
8
=
1
組卷：182引用：7難度：0.6
解析
6．已知三個數1，a,9成等比數列，則圓錐曲線
x
2
a
+
y
2
2
=
1
的離心率為（　　）
A．
3
3
B．
5
C．
5
或
10
2
D．
3
3
或
10
2
組卷：546引用：12難度：0.7
解析
7．函數f（x）=xln（x+2）的圖象在點（-1，0）處的切線與直線（a-2）x+y-2=0垂直，則實數a的值為（　　）
A．-2 B．-1 C．1 D．2
組卷：258引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

21．數列{a_n}是單調遞增的等比數列，a₂=4，a₁+a₂+a₃=14，數列{b_n}滿足b₁=
1
a
1
，且b_n+1=
b
n
3
b
n
+
1
．
（1）證明：數列
{
1
b
n
}
是等差數列，并求{a_n}，{b_n}的通項公式；
（2）設數列
{
a
n
b
n
}
的前n項和為T_n，求T_n．
組卷：206引用：2難度：0.5
解析
22．如圖，橢圓
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的離心率為
3
2
，其短軸和長軸的端點分別為A，B，C，D，且|AB|=2．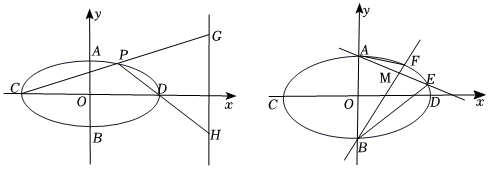

（1）求橢圓的方程；
（2）P是橢圓上位于x軸上方的動點，直線CP，DP與直線l：x=4分別交于G、H兩點．若|GH|=4，求點P的坐標；
（3）直線AM，BM分別與橢圓交于E，F兩點，其中點
M
（
t
,
1
2
）
滿足t≠0且t≠±
3
．若△BME面積是△AMF面積的5倍，求t的值．
組卷：140引用：2難度：0.3
解析