2021-2022學(xué)年陜西省西安市未央?yún)^(qū)博愛國際學(xué)校高二（上）期末數(shù)學(xué)試卷（理科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知命題p：對任意x∈R，都有sinxcosx≤

  1

  2

  ，則?p是（　　）

  A．存在x∈R，使得sinxcosx≤ 1 2

  B．存在x∈R，使得sinxcosx＞ 1 2

  C．對任意x∈R，都有sinxcosx＞ 1 2

  D．對任意x∈R，都有 sinx cosx ＞ 1 2
  組卷：52引用：3難度：0.7

  解析

• 2．若

  1

  a

  ＞

  1

  b

  ，a-b＞0，則（　　）

  A．a(chǎn)＞0＞b	B．a(chǎn)＞b＞0
  C．0＞b＞a	D．無法判斷a,b的正負(fù)
  組卷：203引用：5難度：0.8

  解析

• 3．已知雙曲線C：

  x

  2

  4

  -

  y

  2

  32

  =

  1

  ，則C的離心率為（　　）

  A． 2 14 7

  B． 3 2 4

  C．2

  D．3
  組卷：152引用：3難度：0.9

  解析

• 4．若a＞0，b＞0，且a+2b=1，則

  1

  a

  +

  8

  b

  的最小值是（　　）

  A．8

  B．25

  C．18

  D．20
  組卷：665引用：1難度：0.7

  解析

• 5．“

  x

  -

  1

  x

  ≤

  0

  ”是“x（x-1）≤0”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：51引用：5難度：0.8

  解析

• 6．已知{

  a

  ，

  b

  ，

  c

  }是空間的一個基底，若

  m

  =

  a

  +

  2

  b

  -

  3

  c

  ，

  n

  =

  x

  （

  a

  +

  b

  ）

  -

  y

  （

  b

  +

  c

  ）

  +

  3

  （

  a

  +

  c

  ）

  ，若

  m

  ∥

  n

  ，則

  x

  y

  =（　　）

  A．-3

  B． - 1 3

  C．3

  D． 1 3
  組卷：196引用：3難度：0.6

  解析

• 7．已知拋物線C：y²=2px（p＞0）的焦點(diǎn)為F，點(diǎn)P（2，y₀）在拋物線C上，且

  |

  PF

  |

  =

  3

  p

  4

  ，則p=（　　）

  A．4

  B．6

  C．8

  D．10
  組卷：378引用：10難度：0.7

  解析

三、解答題：本大題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

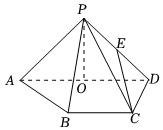• 21．如圖所示的四棱錐P-ABCD的底面ABCD是一個等腰梯形，AD∥BC，且AD=2AB=2BC=4，PO是△PAD的中線，點(diǎn)E是棱PD的中點(diǎn)．
  （1）證明：CE∥平面PAB．
  （2）若平面PAD⊥平面ABCD，且PA=PD，PO=AO，求直線PC與平面PAB所成角的正弦值．
  組卷：157引用：2難度：0.4

  解析

• 22．已知焦點(diǎn)為F的拋物線C：y²=2px（p＞0）上一點(diǎn)P（2，t）到F的距離是4．
  （1）求拋物線C的方程；
  （2）若不過原點(diǎn)O的直線l與拋物線C交于A，B兩點(diǎn)（A，B位于x軸兩側(cè)），C的準(zhǔn)線l′與x軸交于點(diǎn)E，直線OA，OB與l′分別交于點(diǎn)M，N，若|ME|?|NE|=8，證明：直線l過定點(diǎn)．
  組卷：80引用：6難度：0.6

  解析