2021-2022學年浙江省杭州九中高一（上）期末數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項符合題目要求.

• 1．已知集合A={-1，0，1}，B={-1，0，1，2}，則（　　）

  A．A?B

  B．B?A

  C．A∈B

  D．B∈A
  組卷：102引用：5難度：0.9

  解析

• 2．“x＜-1”是“2^x≤1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：50引用：2難度：0.8

  解析

• 3．下列函數中，同一個函數的定義域與值域相同的是（　　）

  A．y= x - 1

  B．y= 2 x + 1 x - 1

  C．y= 1 2 x - 1

  D．y=10lgx
  組卷：152引用：3難度：0.8

  解析

• 4．已知角θ的終邊經過點M（m,2-m），且

  tanθ

  =

  1

  3

  ，則m=（　　）

  A． 3 2

  B． 1 2

  C．-1

  D．3
  組卷：249引用：2難度：0.7

  解析

• 5．cos105°=（　　）

  A． 2 - 3 4

  B． 2 + 3 4

  C． 2 - 6 4

  D． 6 - 2 4
  組卷：472引用：7難度：0.8

  解析

• 6．若不等式ax²+bx+c＞0的解集為{x|-2＜x＜3}，那么不等式a（x²+1）+b（x-1）+c＞2ax的解集為（　　）

  A．{x|-3＜x＜2}

  B．{x|x＜-3或x＞2}

  C．{x|-1＜x＜4}

  D．{x|x＜-1或x＞4}
  組卷：443引用：3難度：0.7

  解析

• 7．已知x₀是函數f（x）=2^x+x-1的一個零點．若x₁∈（-1，x₀），x₂∈（x₀，+∞），則（　　）

  A．f（x1）＜0，f（x2）＜0	B．f（x1）＞0，f（x2）＜0
  C．f（x1）＜0，f（x2）＞0	D．f（x1）＞0，f（x2）＞0
  組卷：123引用：7難度：0.7

  解析

四、解答題：本大題共6小題，共70分，解答應寫出必要的文字說明、證明過程或演算步驟.

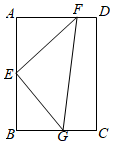• 21．如圖，在矩形ABCD中，AB=2，AD=

  3

  ，點E為AB的中點，F，G分別為線段AD，BC上的點，且EF⊥EG，∠AEF=θ．
  （1）若△EFG的周長為f（θ），求f（θ）的解析式及θ的取值范圍；
  （2）求f（θ）的最值．
  組卷：132引用：8難度：0.5

  解析

• 22．定義：若函數f（x）對于其定義域內的某一數x₀，有f（x₀）=x₀，則稱x₀是f（x）的一個不動點，已知函數f（x）=ax²+（b+1）x+b-1（a≠0）．
  （1）當a=1，b=3時，求函數f（x）的不動點；
  （2）若對任意的實數b,函數f（x）恒有兩個不動點，求a的取值范圍；
  （3）在（2）的條件下，若y=f（x）圖象上兩個點A、B的橫坐標是函數f（x）的不動點，且A、B的中點C在函數

  g

  （

  x

  ）

  =

  -

  x

  +

  2

  a

  5

  a

  2

  -

  4

  a

  +

  1

  的圖象上，求b的最小值．
  組卷：130引用：8難度：0.3

  解析