2021-2022學年江西省上饒市余干縣八校聯(lián)考九年級(下)期中數(shù)學試卷
發(fā)布:2024/4/20 14:35:0
一、選擇題(共6小題,每小題3分,共18分)
-
1.下列數(shù)中,是無理數(shù)的是( )
A.-3 B.0 C. 13D. 7組卷:560引用:12難度:0.9 -
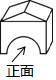 2.老師用兩塊積木搭建的幾何體如圖所示,則這個幾何體的左視圖是( )
2.老師用兩塊積木搭建的幾何體如圖所示,則這個幾何體的左視圖是( )A. 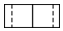
B. 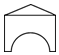
C. 
D. 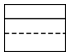 組卷:187引用:4難度:0.9
組卷:187引用:4難度:0.9 -
3.7名學生的鞋號(單位:厘米)由小到大是:20,21,22,22,22,23,23,則這組數(shù)據(jù)的眾數(shù)和中位數(shù)分別是( )
A.20,21 B.21,22 C.22,22 D.22,23 組卷:307引用:7難度:0.8 -
4.下列計算正確的是( )
A.-2a+4a=-2a B.-2a2b?3a3=-6a6b C.(2a2b)2=2a4b2 D.6a6b÷(-2a2b)=-3a4 組卷:29引用:1難度:0.8 -
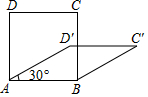 5.四邊形具有不穩(wěn)定性,對于四條邊長確定的四邊形.當內(nèi)角度數(shù)發(fā)生變化時,其形狀也會隨之改變.如圖,改變正方形ABCD的內(nèi)角,正方形ABCD變?yōu)榱庑蜛BC′D′.若∠D′AB=30°,則菱形ABC′D′的面積與正方形ABCD的面積之比是( )
5.四邊形具有不穩(wěn)定性,對于四條邊長確定的四邊形.當內(nèi)角度數(shù)發(fā)生變化時,其形狀也會隨之改變.如圖,改變正方形ABCD的內(nèi)角,正方形ABCD變?yōu)榱庑蜛BC′D′.若∠D′AB=30°,則菱形ABC′D′的面積與正方形ABCD的面積之比是( )A.1 B. 12C. 22D. 32組卷:1662引用:21難度:0.9 -
6.已知拋物線y=(x-m)(x-n),其中m<n,若a,b是方程(x-m)(x-n)-x=0的兩根,且a<b,則當(a-m)(b-n)>0時,mn的值( )
A.小于零 B.等于零 C.大于零 D.與零的大小關系無法確定 組卷:501引用:4難度:0.7
二、填空題(共6小題,每小題3分,共18分)
-
7.計算:(1-2a)(2a-1)=
.組卷:130引用:2難度:0.9 -
8.若關于x的一元二次方程x2-2x+m=0有一個解為x=-1,則另一個解為.
組卷:468引用:8難度:0.8
五、(本大題共2小題,每小題9分,共18分)
-
23.在一堂數(shù)學實踐課上,趙老師給出了下列問題:
【提出問題】
(1)如圖1,在△ABC中,E是BC的中點,P是AE的中點,就稱CP是△ABC的“雙中線”,∠ACB=90°,AC=3,AB=5.則CP=.
【探究規(guī)律】
(2)在圖2中,E是正方形ABCD一邊上的中點,P是BE上的中點,則稱AP是正方形ABCD的“雙中線”,若AB=4.則AP的長為(按圖示輔助線求解);
(3)在圖3中,AP是矩形ABCD的“雙中線”,若AB=4,BC=6,請仿照(2)中的方法求出AP的長,并說明理由;
【拓展應用】
(4)在圖4中,AP是平行四邊形ABCD的“雙中線”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周長,并說明理由? 組卷:494引用:9難度:0.1
組卷:494引用:9難度:0.1
六、(本大題共12分)
-
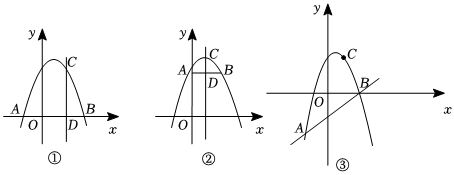
24.在平面直角坐標系中,直線AB與拋物線y=ax2+bx+c交于A,B(點A在點B的左側(cè))兩點,點C是該拋物線上任意一點,過C點作平行于y軸的直線交AB于D,分別過點A,B作直線CD的垂線,垂足分別為點E,F(xiàn).
特例感悟:
(1)已知:a=-2,b=4,c=6.
①如圖①,當點C的橫坐標為2,直線AB與x軸重合時,CD=,|a|?AE?BF=.
②如圖②,當點C的橫坐標為1,直線AB∥x軸且過拋物線與y軸的交點時,CD=,|a|?AE?BF=.
③如圖③,當點C的橫坐標為2,直線AB的解析式為y=x-3時,CD=,|a|?AE?BF=.
猜想論證:
(2)由(1)中三種情況的結(jié)果,請你猜想在一般情況下CD與|a|?AE?BF之間的數(shù)量關系,并證明你的猜想.拓展應用.
(3)若a=-1,點A,B的橫坐標分別為-4,2,點C在直線AB的上方的拋物線上運動(點C不與點A,B重合),在點C的運動過程中,利用(2)中的結(jié)論求出△ACB的最大面積.組卷:21引用:2難度:0.3


