2023-2024學年河南省濮陽市高二（上）月考數學試卷（9月份）

一、單項選擇題（共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.）

• 1．已知空間向量

  a

  =

  （

  4

  ，-

  1

  ，

  1

  ）

  ，

  b

  =

  （

  x

  ,

  y

  ,

  2

  ）

  ，且

  a

  ∥

  b

  ，則x+y=（　　）

  A．6

  B．10

  C．8

  D．4
  組卷：54引用：3難度：0.7

  解析

• 2．如圖，設

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，若

  AN

  =

  NB

  ，

  BM

  =

  3

  MC

  ，則

  MN

  =（　　）

  A． 1 2 a + 1 4 b - 3 4 c	B． - 1 2 a - 1 4 b + 3 4 c
  C． 1 2 a - 1 4 b - 1 4 c	D． - 1 2 a + 1 4 b + 1 4 c
  組卷：55引用：4難度：0.7

  解析

• 3．若直線l的方向向量為

  e

  =

  （

  2

  ，

  3

  ，-

  1

  ）

  ，平面α的法向量為

  n

  =

  （

  -

  1

  ，-

  3

  2

  ，

  1

  2

  ）

  ，則直線l和平面α的位置關系是（　　）

  A．l⊥α

  B．l∥α

  C．l∥α或l?α

  D．l?α
  組卷：242引用：6難度：0.7

  解析

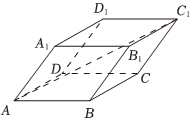• 4．已知平行六面體ABCD-A₁B₁C₁D₁的各棱長均為1，∠A₁AB=∠A₁AD=45°，∠DAB=90°，則

  |

  A

  C

  1

  |

  =（　　）

  A． 3

  B． 2 + 2

  C． 2

  D． 2 + 1
  組卷：19引用：2難度：0.7

  解析

• 5．已知經過點A（1，2，3）的平面α的法向量為

  n

  =（1，-1，1），則點P（-2，3，1）到平面α的距離為（　　）

  A． 3

  B．2

  C． 2 2

  D． 2 3
  組卷：76引用：8難度：0.7

  解析

• 6．在平行六面體ABCD-A₁B₁C₁D₁中，底面ABCD是邊長為2的正方形，AA₁=4，∠A₁AD=∠A₁AB=60°，則異面直線AC與DC₁直線所成角的余弦值為（　　）

  A． 14 7

  B． 70 14

  C． 3 14 14

  D． 11 14 14
  組卷：106引用：5難度：0.7

  解析

• 7．已知正四面體ABCD，M為BC中點，N為AD中點，則直線BN與直線DM所成角的余弦值為（　　）

  A． 1 6

  B． 2 3

  C． 21 21

  D． 4 21 21
  組卷：184引用：10難度：0.7

  解析

四、解答題：本題共6小題，70分，其中第17題10分，其余均12分.

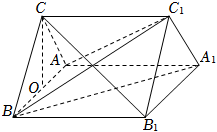• 21．如圖，直三棱柱ABC-A₁B₁C₁中，ABC是邊長為2的正三角形，O為AB的中點．
  （1）證明：CO⊥平面ABB₁A₁；
  （2）若直線B₁C與平面ABB₁A₁所成的角的正切值為

  15

  5

  ，求平面A₁BC₁與平面ABC₁夾角的余弦值．
  組卷：126引用：8難度：0.4

  解析

• 22．長方形ABCD中，AB=2AD，M是DC中點（圖1）．將△ADM沿AM折起，使得AD⊥BM（圖2）．在圖2中：
  
  （1）求證：平面ADM⊥平面ABCM；
  （2）在線段BD上是否存在點E，使得二面角E-AM-D為大小為

  π

  4

  ，說明理由．
  組卷：112引用：7難度：0.3

  解析