當前位置：試卷中心 > 試卷詳情

2021-2022學年河北省保定市博野中學高二（上）期中數學試卷

發布：2024/12/3 20:0:1

一、單項選擇題（本大題共8小題，每小題5分，共40.0分）

1．設p：-1≤x＜2，q：x＜a,若q是p的必要條件，則a的取值范圍是（　　）
A．a≤-1 B．a≤-1或a≥2 C．a≥2 D．-1≤a＜2
組卷：28引用：4難度：0.9
解析
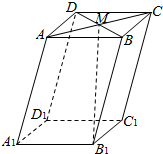2．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，M為AC與BD的交點，若
A
1
B
1
=
a
，
A
1
D
1
=
b
，
A
1
A
=
c
．則下列向量中與
B
1
M
相等的向量是（　　）
A．-
1
2
a
+
1
2
b
+
c
B．
1
2
a
+
1
2
b
+
c
C．
1
2
a
-
1
2
b
+
c
D．-
1
2
a
-
1
2
b
+
c
組卷：1928引用：110難度：0.9
解析
3．已知
a
=
（
-
3
，
2
，
5
）
，
b
=
（
1
，
x
,-
1
）
，且
a
?
b
=2，則x的值為（　　）
A．3 B．4 C．5 D．6
組卷：1083引用：15難度：0.9
解析
4．已知向量
a
=（0，-1，1），
b
（4，1，0），|λ
a
+
b
|=
29
且λ＞0，則λ=（　　）
A．-2 B．2 C．-3 D．3
組卷：390引用：8難度：0.9
解析
5．已知橢圓C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的左、右焦點為F₁、F₂，離心率為
3
3
，過F₂的直線l交C于A、B兩點，若△AF₁B的周長為4
3
，則C的方程為（　　）
A．
x
2
3
+
y
2
2
=1 B．
x
2
3
+y²=1 C．
x
2
12
+
y
2
8
=1 D．
x
2
12
+
y
2
4
=1
組卷：8985引用：113難度：0.9
解析
6．正三棱錐P-ABC的側面都是直角三角形，E，F分別是AB，BC的中點，則PB與平面PEF所成角的正弦值為（　　）
A．
3
6
B．
6
6
C．
3
3
D．
6
3
組卷：2945引用：10難度：0.4
解析
7．若點O和點F分別為橢圓
x
2
4
+
y
2
3
=1的中心和左焦點，點P為橢圓上的任意一點，則
OP
?
FP
的最大值為（　　）
A．2 B．3 C．6 D．8
組卷：3851引用：119難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共6小題，共70.0分）

21．已知點P是圓Q：（x+2）²+y²=32上任意一點，定點R（2，0），線段PR的垂直平分線l與半徑PQ相交于M點，當P在圓周上運動時，設點M的運動軌跡為Γ．
（1）求點M的軌跡Γ的方程；
（2）若點N在雙曲線
x
2
4
-
y
2
2
=
1
（頂點除外）上運動，過點N、R的直線與曲線Γ相交于A、B，過點N，Q的直線與曲線Γ相交于C、D，試探究|AB|+|CD|是否為定值，若為定值請求出這個定值，若不為定值，請說明理由．
組卷：148引用：4難度：0.4
解析
22．如圖1，在直角梯形ABCD中，AD∥BC，AB⊥BC，BD⊥CD．將△ABD沿BD折起，折起后點A的位置為點P，得到幾何體P-BCD，如圖2所示，且平面PBD⊥平面BCD，
（Ⅰ）證明：PB⊥平面PCD；
（Ⅱ）若AD=2，當PC和平面PBD所成角的正切值為
2
時，試判斷線段BD上是否存在點E，使二面角D-PC-E平面角的余弦值為
42
7
？若存在，請確定其位置；若不存在，請說明理由．
組卷：185引用：3難度：0.7
解析