2022-2023學年遼寧省部分學校聯考高一（下）月考數學試卷（4月份）

一、單選題。（本大題共8小題）

• 1．已知角α的終邊經過點（-1，6），則cosα=（　　）

  A． 6 37 37

  B． - 6 37 37

  C． 37 37

  D． - 37 37
  組卷：246引用：3難度：0.8

  解析

• 2．已知向量

  a

  =

  （

  -

  1

  ，

  7

  ）

  ，

  |

  b

  |

  =

  1

  ，且

  a

  ，

  b

  的夾角為

  π

  4

  ，則

  |

  a

  -

  2

  b

  |

  =（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：69引用：2難度：0.7

  解析

• 3．若

  sinα

  tanα

  ＞

  0

  ，

  tanα

  cosα

  ＜

  0

  ，則α是（　　）

  A．第一象限角

  B．第二象限角

  C．第三象限角

  D．第四象限角
  組卷：178引用：2難度：0.8

  解析

• 4．cos54°cos24°+2sin12°cos12°sin126°=（　　）

  A． 1 2

  B． 2 2

  C． 3 2

  D． 6 - 2 4
  組卷：136引用：2難度：0.8

  解析

• 5．將函數y=tanx圖象上所有點的橫坐標縮短到原來的

  1

  4

  （縱坐標不變），把得到的圖象向左平移

  π

  12

  個單位長度，再把得到的圖象向上平移2個單位長度，得到函數f（x）的圖象，則f（x）圖象的對稱中心為（　　）

  A．（ - π 12 + kπ 4 ，0）（k∈Z）	B．（ - π 12 + kπ 8 ，0）（k∈Z）
  C．（ - π 12 + kπ 4 ，2）（k∈Z）	D．（- π 12 + kπ 8 ，2）（k∈Z）
  組卷：59引用：2難度：0.7

  解析

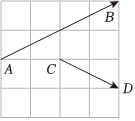• 6．如圖，在4×4正方形網格中，螞蟻甲從A點爬到了B點，螞蟻乙從C點爬到了D點，則向量

  AB

  與

  CD

  夾角的余弦值為（　　）

  A． 1 5

  B． 2 5

  C． 3 5

  D． 4 5
  組卷：74引用：4難度：0.8

  解析

• 7．若a=1.2，b=sin1.2，c=tan1.2，則（　　）

  A．c＞a＞b

  B．c＞b＞a

  C．a＞c＞b

  D．b＞c＞a
  組卷：67引用：2難度：0.5

  解析

四、解答題。（本大題共6小題）

• 21．已知

  0

  ＜

  α

  ＜

  π

  3

  ，

  -

  π

  2

  ＜

  β

  ＜

  -

  π

  3

  ，

  cos

  （

  α

  +

  π

  6

  ）

  =

  3

  3

  ，

  sin

  （

  α

  -

  β

  +

  π

  6

  ）

  =

  2

  3

  ．
  （1）求sinα；
  （2）求cos（3α-β）．
  組卷：83引用：2難度：0.5

  解析

• 22．若函數f（x）滿足

  f

  （

  x

  -

  π

  2

  ）

  =

  f

  （

  x

  +

  π

  2

  ）

  ，且f（a-x）=f（x+a），a∈R，則稱f（x）為“M型a函數”．
  （1）判斷函數

  y

  =

  sin

  （

  2

  x

  -

  π

  4

  ）

  是否為“M型

  3

  π

  8

  函數”，并說明理由；
  （2）已知g（x）為定義域為R的奇函數，當x＞0時，g（x）=lnx,函數h（x）為“M型

  π

  6

  函數”，當

  x

  ∈

  [

  -

  π

  3

  ，

  π

  6

  ]

  時，h（x）=2cos2x,若函數F（x）=g（h（x）-m）（m∈R）在

  [

  -

  5

  π

  6

  ，

  2

  π

  3

  ]

  上的零點個數為9，求m的取值范圍．
  組卷：79引用：6難度：0.6

  解析