2022-2023學年福建省寧德一中高一（下）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一個選項是符合題目要求的.

• 1．已知復數z滿足

  z

  i

  +

  1

  =

  2

  i

  ，則z=（　　）

  A．2-i

  B．2+i

  C．-2-i

  D．-2+i
  組卷：22引用：2難度：0.9

  解析

• 2．下圖是某商場2022年洗衣機、電視機和電冰箱三種電器各季度銷量的百分比堆積圖（例如：第三季度內，洗衣機銷量約占20%，電視機銷量約占50%，電冰箱銷量約占30%）．根據該圖，以下結論中正確的是（　　）
  

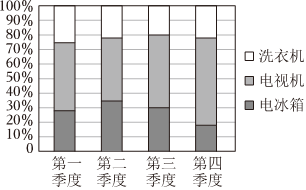
  A．電視機銷量最大的是第四季度

  B．電冰箱銷量最小的是第四季度

  C．電視機的全年銷量最大

  D．洗衣機的全年銷量最小
  組卷：15引用：2難度：0.7

  解析

• 3．已知三個不同的平面α，β，γ和兩條不重合的直線m,n,則下列四個命題中正確的是（　　）

  A．若m∥α，α∩β=n,則m∥n

  B．若α∩β=n,m?α，m⊥n,則α⊥β

  C．若α⊥β，γ⊥β，則α∥γ

  D．若α∩β=m,m⊥γ，則α⊥γ
  組卷：210引用：7難度：0.6

  解析

• 4．已知圓錐PO，其軸截面（過圓錐旋轉軸的截面）是底邊長為6m,頂角為

  2

  π

  3

  的等腰三角形，該圓錐的側面積為（　　）

  A．6πm2

  B． 6 3 π m 2

  C． 3 3 π m 2

  D． 12 3 π m 2
  組卷：106引用：3難度：0.8

  解析

• 5．在達州市北部的鳳凰山上有一座標志性建筑-鳳凰樓，某同學為測量鳳凰樓的高度MN，在鳳凰樓的正北方向找到一座建筑物AB，高約為22.5m,在地面上點C處（B，C，N三點共線）測得建筑物頂部A，鳳凰樓頂部M的仰角分別為30°和45°，在A處測得鳳凰樓頂部M的仰角為15°，鳳凰樓的高度約為（　　）
  

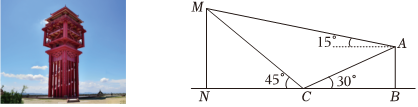
  A．32m

  B．39m

  C．45m

  D．55m
  組卷：114引用：5難度：0.7

  解析

• 6．我國古代數學名著《九章算術》中記載的“芻甍”（chumeng）是指底面為矩形，頂部只有一條棱的五面體．如圖，五面體ABCDEF是一個芻甍，其中△BCF是正三角形，AB=2BC=2EF，則以下兩個結論：①AB∥EF；②BF⊥ED，（　　）

  A．①和②都不成立	B．①成立，但②不成立
  C．①不成立，但②成立	D．①和②都成立
  組卷：753引用：10難度：0.9

  解析

• 7．已知某樣本的容量為50，平均數為70，方差為75．現發現在收集這些數據時，其中的兩個數據記錄有誤，一個錯將80記錄為60，另一個錯將70記錄為90．在對錯誤的數據進行更正后，重新求得樣本的平均數為

  x

  ，方差為s²，則（　　）

  A． x =70，s2＜75

  B． x =70，s2＞75

  C． x ＞70，s2＜75

  D． x ＜70，s2＞75
  組卷：619引用：24難度：0.9

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

• 21．如圖，在正方形ABCD中，點E是AB的中點，點F是BC的中點，將△AED，△DCF分別沿DE，DF折起，使A，C兩點重合于P，連接EF，PB．
  （1）求證：PB⊥EF；
  （2）點M是PD上一點，若PB∥平面EFM，則

  |

  PM

  |

  |

  MD

  |

  為何值？并說明理由；
  （3）若MD=3PM，求二面角M-EF-D的余弦值．
  組卷：46引用：4難度：0.5

  解析

• 22．甲，乙兩人進行圍棋比賽，采取積分制，規則如下：每勝1局得1分，負1局或平局都不得分，積分先達到2分者獲勝；若第四局結束，沒有人積分達到2分，則積分多的一方獲勝；若第四局結束，沒人積分達到2分，且積分相等，則比賽最終打平．假設在每局比賽中，甲勝的概率為

  1

  2

  ，負的概率為

  1

  3

  ，且每局比賽之間的勝負相互獨立．
  （1）求第三局結束時乙獲勝的概率；
  （2）求甲獲勝的概率．
  組卷：267引用：13難度：0.7

  解析