2022-2023學(xué)年福建省福州市晉安區(qū)鼓山中學(xué)高三（上）月考數(shù)學(xué)試卷（11月份）

一、單項選擇題（本大題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的）.

• 1．已知集合A={x|x²-5x-6≤0}，B={x|2^x-1≥1}，則A∩B=（　　）

  A．[1，6]

  B．[1，3]

  C．[-1，1]

  D．[2，3]
  組卷：13引用：5難度：0.8

  解析

• 2．若復(fù)數(shù)

  a

  +

  bi

  4

  +

  3

  i

  （i為虛數(shù)單位，a,b∈R且b≠0）為純虛數(shù)，則

  a

  b

  =（　　）

  A． 4 3

  B． - 4 3

  C． 3 4

  D． - 3 4
  組卷：429引用：12難度：0.9

  解析

• 3．已知雙曲線x²-

  y

  2

  24

  =1的兩個焦點為F₁，F(xiàn)₂，P為雙曲線右支上一點．若|PF₁|=

  4

  3

  |

  P

  F

  2

  |，則△F₁PF₂的面積為（　　）

  A．48

  B．24

  C．12

  D．6
  組卷：409引用：5難度：0.7

  解析

• 4．函數(shù)y=

  sin

  2

  x

  1

  -

  cosx

  的部分圖象大致為（　　）

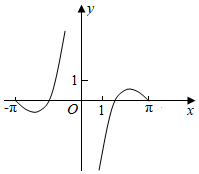
  A．	B．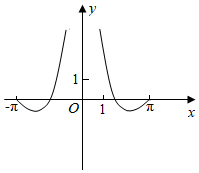
  C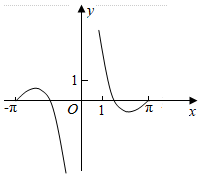．	D．
  組卷：7592引用：48難度：0.7

  解析

• 5．已知△ABC中，角A，B，C的對邊分別為a,b,c,且

  a

  =

  2

  ，

  b

  =

  6

  ，

  A

  =

  30

  °

  ，則c=（　　）

  A． 2

  B． 2 2

  C． 2 或 2 2

  D．2或 3
  組卷：258引用：8難度：0.7

  解析

• 6．我國古代數(shù)學(xué)家僧一行應(yīng)用“九服晷影算法”在《大衍歷》中建立了晷影長l與太陽天頂距θ（0°≤θ≤180°）的對應(yīng)數(shù)表，這是世界數(shù)學(xué)史上較早的一張正切函數(shù)表．根據(jù)三角學(xué)知識可知，晷影長度l等于表高h(yuǎn)與太陽天頂距θ正切值的乘積，即l=htanθ．對同一“表高”兩次測量，第一次和第二次太陽天頂距分別為α，β，若第一次晷影長是“表高”的2倍，且

  tan

  （

  α

  -

  β

  ）

  =

  1

  3

  ，則第二次的晷影長是“表高”的（　　）倍．

  A．1

  B．2

  C．3

  D．4
  組卷：94引用：4難度：0.6

  解析

• 7．設(shè)

  a

  =

  5

  sin

  1

  5

  ，

  b

  =

  cos

  1

  10

  ，

  c

  =

  10

  sin

  1

  10

  ，則（　　）

  A．c＜b＜a

  B．b＜a＜c

  C．a(chǎn)＜c＜b

  D．a(chǎn)＜b＜c
  組卷：107引用：3難度：0.6

  解析

四、解答題（共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟）.

• 21．已知函數(shù)

  f

  （

  x

  ）

  =

  8

  -

  4

  x

  x

  2

  -

  2

  x

  +

  m

  ．
  （1）若m=-2，求曲線y=f（x）在（2，f（2））處的切線方程；
  （2）若x=0為函數(shù)f（x）的極值點，且函數(shù)g（x）=f（x）-λ有兩個零點，求實數(shù)λ的取值范圍．
  組卷：30引用：2難度：0.4

  解析

• 22．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為e,且

  2

  b

  2

  a

  與e為方程2x²-7x+3=0的兩根．
  （1）求橢圓C的方程；
  （2）過右焦點F₂且斜率為k的直線l與橢圓交于不同的兩點M、N，l₀與l關(guān)于x軸對稱，Q是l₀與y軸的交點，若

  |

  2

  QM

  +

  QN

  |

  =

  |

  2

  QM

  -

  QN

  |

  ，求k²的值．
  組卷：3引用：2難度：0.6

  解析