當前位置：試卷中心 > 試卷詳情

2022-2023學年安徽省安慶市桐城中學高一（上）第二次月考數學試卷

發布：2024/8/3 8:0:9

一、選擇題（共8小題，每小題5分，滿分40分）

1．設全集U=R，集合A={x|-1＜x＜3}，B={x|x-1≥0}，則?_U（A∩B）=（　　）
A．{x|1≤x＜3} B．{x|1＜x≤3} C．{x|x≤1或x≥3} D．{x|x＜1或x≥3}
組卷：2引用：3難度：0.7
解析
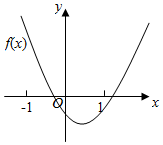2．已知函數f（x）=（x-a）（x-b）（其中a＞b）的圖象如圖所示，則函數g（x）=a^x+b的圖象是（　　）
A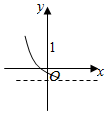． B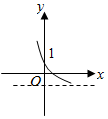． C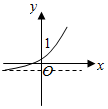． D．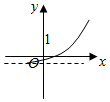
組卷：1303引用：213難度：0.9
解析
3．已知函數
f
（
x
）
=
lo
g
0
.
5
（
x
2
-
ax
+
3
a
）
在（2，+∞）上單調遞減，則實數a的取值范圍（　　）
A．（-∞，4] B．[4，+∞） C．[-4，4] D．（-4，4]
組卷：103引用：15難度：0.8
解析
4．已知函數f（x）=2^x+x-1，g（x）=log₂x+x-1，h（x）=x³+x-1的零點分別為a,b,c,則a,b,c的大小為（　　）
A．c＞b＞a B．b＞c＞a C．c＞a＞b D．a＞c＞b
組卷：291引用：3難度：0.7
解析
5．已知函數
f
（
x
）
=
ln
（
1
+
x
2
）
-
1
1
+
|
x
|
，若實數a滿足
f
（
lo
g
3
a
）
+
f
（
lo
g
1
3
a
）
≤
2
f
（
1
）
，則a的取值范圍（　　）
A．[1，3] B．
（
0
，
1
3
]
C．（0，3] D．
[
1
3
，
3
]
組卷：1260引用：4難度：0.6
解析
6．已知f（x）=
2
x
2
+
3
x
+
1
，
x
≤
0
|
lo
g
2
x
|
，
x
＞
0
，函數g（x）=f（x）+b有四個不同的零點x₁，x₂，x₃，x₄，且滿足：x₁＜x₂＜x₃＜x₄．則下列結論中不正確的是（　　）
A．-1＜b＜0 B．x₃x₄=1 C．
1
2
≤
x
3
＜
1
D．
x
1
+
x
2
=
-
3
2
組卷：182引用：8難度：0.6
解析
7．若函數f（x+2）為偶函數，對任意，x₁，x₂∈[2，+∞），且x₁≠x₂，都有（x₁-x₂）[f（x₁）-f（x₂）]＞0，則（　　）
A．
f
（
log
2
6
）
＜
f
（
3
2
）
＜
f
（
log
3
12
）
B．
f
（
log
3
12
）
＜
f
（
3
2
）
＜
f
（
log
2
6
）
C．
f
（
log
3
12
）
＜
f
（
log
2
6
）
＜
f
（
3
2
）
D．
f
（
3
2
）
＜
f
（
log
2
6
）
＜
f
（
log
3
12
）
組卷：62引用：6難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（共6小題，滿分70分）

21．已知函數
f
（
x
）
=
lo
g
4
（
4
x
+
1
）
-
1
2
x
,
x
∈
R
．
（1）若函數f（x）的圖象與直線
y
=
1
2
x
+
a
沒有公共點，求a的取值范圍；
（2）若函數
g
（
x
）
=
4
f
（
x
）
+
x
2
+
m
?
2
x
-
1
，
x
∈
[
0
，
lo
g
2
3
]
，是否存在m,使g（x）最小值為0．若存在，求出m的值；若不存在，說明理由．
組卷：9引用：2難度：0.5
解析
22．已知定義在R上的函數f（x）滿足f（-x）-f（x）=0，且
f
（
x
）
=
lo
g
2
（
2
x
+
1
）
+
kx
，g（x）=f（x）+x.
（1）求f（x）的解析式；
（2）若不等式g（4^x-a?2^x+1）＞g（-3）恒成立，求實數a的取值范圍；
（3）設h（x）=x²-2mx+1，若對任意的x₁∈[0，3]，存在x₂∈[1，3]，使得g（x₁）≥h（x₂），求實數m的取值范圍．
組卷：202引用：21難度：0.6
解析