當(dāng)前位置：試卷中心 > 試卷詳情

2023年湖南省九校聯(lián)盟高考數(shù)學(xué)第二次聯(lián)考試卷

發(fā)布：2024/4/20 14:35:0

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項(xiàng)中，只有一個是符合題目要求的.

1．已知集合A={x||x-1|＜1}，B={x|x≥a}，且A?B，則實(shí)數(shù)a的取值范圍為（　　）
A．（-∞，1） B．（-∞，0] C．[0，+∞） D．[1，+∞）
組卷：277引用：4難度：0.9
解析
2．在復(fù)數(shù)范圍內(nèi)解得方程x²+4x+5=0的兩根為x₁，x₂，則|x₁-x₂|=（　　）
A．4 B．1 C．2 D．3
組卷：79引用：2難度：0.7
解析

3．已知函數(shù)f（x）=log₂|cosx|，則下列論述正確的是（　　）

A．?x₁，x₂∈（0，2π）且x₁≠x₂，使f（x₁）+f（x₂）=0

B．

，

∈

（

，

]

，當(dāng)x₁＜x₂時，有f（x₁）＜f（x₂）恒成立

C．使f（x）有意義的必要不充分條件為

∈

{

∈

≠

kπ

，

∈

}

D．使

（

）

≥

成立的充要條件為

∈

{

∈

≤

}

組卷：76引用：1難度：0.5

解析

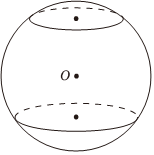4．如圖所示，一個球內(nèi)接圓臺，已知圓臺上、下底面的半徑分別為3和4，球的表面積為100π，則該圓臺的體積為（　　）
A．
175
π
3
B．75π C．
238
π
3
D．
259
π
3
組卷：449引用：7難度：0.6
解析
5．兩千多年前，古希臘數(shù)學(xué)家阿波羅尼斯采用切割圓錐的方法研究圓錐曲線，他用平行于圓錐的軸的平面截取圓錐得到的曲線叫做“超曲線”，即雙曲線的一支，已知圓錐PQ的軸截面為等邊三角形，平面α∥PQ，平面α截圓錐側(cè)面所得曲線記為C，則曲線C所在雙曲線的離心率為（　　）
A．
2
3
3
B．
13
3
C．
3
D．2
組卷：195引用：4難度：0.7
解析

6．下列關(guān)于統(tǒng)計概率知識的判斷，正確的是（　　）

A．將總體劃分為2層，通過分層隨機(jī)抽樣，得到兩層的樣本平均數(shù)和樣本方差分別為

，

和

，

，且已知

，則總體方差

（

）

B．在研究成對數(shù)據(jù)的相關(guān)關(guān)系時，相關(guān)關(guān)系越強(qiáng)，相關(guān)系數(shù)r越接近于1

C．已知隨機(jī)變量X服從正態(tài)分布N（μ，σ²），若P（X≥-1）+P（X≥5）=1，則μ=2

D．按從小到大順序排列的兩組數(shù)據(jù)：甲組：27，30，37，m,40，50；乙組：24，n,33，44，48，52，若這兩組數(shù)據(jù)的第30百分位數(shù)、第50百分位數(shù)都分別對應(yīng)相等，則m+n=67

組卷：474引用：3難度：0.5

解析

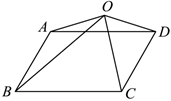7．如圖，O是平行四邊形ABCD所在平面內(nèi)的一點(diǎn)，且滿足
∠
AOB
=
1
2
∠
BOC
=
π
6
，
2
3
|
OA
|
=
2
|
OB
|
=
3
|
OC
|
=
6
，則
|
OD
|
=（　　）
A．2 B．
3
C．
2
D．1
組卷：295引用：2難度：0.7
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

21．在平面直角坐標(biāo)系xOy中，已知橢圓
W
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的離心率為
2
2
，橢圓W上的點(diǎn)與點(diǎn)P（0，2）的距離的最大值為4．
（1）求橢圓W的標(biāo)準(zhǔn)方程；
（2）點(diǎn)B在直線x=4上，點(diǎn)B關(guān)于x軸的對稱點(diǎn)為B₁，直線PB，PB₁分別交橢圓W于C，D兩點(diǎn)（不同于P點(diǎn)）．求證：直線CD過定點(diǎn)．
組卷：185引用：2難度：0.3
解析
22．已知
f
（
x
）
=
1
2
x
2
-
x
-
aln
（
x
-
a
）
，
a
∈
R
．
（1）判斷函數(shù)f（x）的單調(diào)性；
（2）若x₁，x₂是函數(shù)
g
（
x
）
=
f
（
x
+
a
）
-
a
（
x
+
1
2
a
-
1
）
的兩個極值點(diǎn)，且x₁＜x₂，求證：
0
＜
f
（
x
1
）
-
f
（
x
2
）
＜
1
2
．
組卷：291引用：3難度：0.6
解析