2021-2022學年湖南省長沙市長郡中學高一（下）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一個選項是符合題目要求的．

• 1．當

  2

  3

  ＜m＜1時，復數m（3+i）-（2+i）在復平面內對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：532引用：62難度：0.9

  解析

• 2．已知

  AB

  =

  a

  +

  5

  b

  ，

  BC

  =

  -

  2

  a

  +

  8

  b

  ，

  CD

  =

  3

  （

  a

  -

  b

  ）

  ，則（　　）

  A．A、B、D三點共線	B．A、B、C三點共線
  C．B、C、D三點共線	D．A、C、D三點共線
  組卷：893引用：37難度：0.9

  解析

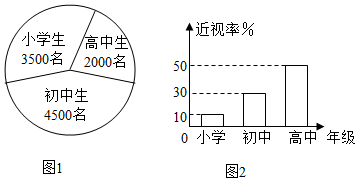• 3．已知某地區中小學生人數和近視情況分別如圖1和圖2所示．為了了解該地區中小學生的近視形成原因，用分層抽樣的方法抽取2%的學生進行調查，則樣本容量和抽取的高中生近視人數分別為（　　）

  A．200，20

  B．100，20

  C．200，10

  D．100，10
  組卷：1501引用：47難度：0.9

  解析

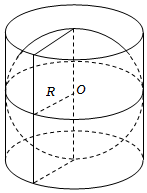• 4．如圖，已知圓柱的底面直徑和高都等于球的直徑，圓柱的表面積為54π，則球的體積為（　　）

  A．27π

  B．36π

  C．54π

  D．108π
  組卷：298引用：4難度：0.7

  解析

• 5．生物實驗室有5只兔子，其中只有3只測量過某項指標．若從這5只兔子中隨機取出3只，則恰有2只測量過該指標的概率為（　　）

  A． 2 3

  B． 3 5

  C． 2 5

  D． 1 5
  組卷：4922引用：33難度：0.8

  解析

• 6．在四棱柱ABCD-A₁B₁C₁D₁中，A₁A⊥平面ABCD，AA₁=3，底面是邊長為4的菱形，且∠DAB=60°，AC∩BD=O，A₁C₁∩B₁D₁=O₁，E是O₁A的中點，則點E到平面O₁BC的距離為（　　）

  A．2

  B．1

  C． 3 2

  D．3
  組卷：130引用：6難度：0.6

  解析

• 7．四名同學各擲骰子5次，分別記錄每次骰子出現的點數，根據四名同學的統計結果，可以判斷出一定沒有出現點數6的是（　　）

  A．平均數為3，中位數為2	B．中位數為3，眾數為2
  C．平均數為2，方差為2.4	D．中位數為3，方差為2.8
  組卷：775引用：33難度：0.8

  解析

四、解答題：本題共6小題，共70分．應寫出文字說明、證明過程或演算步驟．

• 21．記△ABC的內角A，B，C的對邊分別為a,b,c.已知sinC=2sinAsinB，點D在邊AB上，且CD⊥AB．
  （1）證明：CD=

  1

  2

  c；
  （2）若a²+b²=

  6

  ab,求∠ACB．
  組卷：500引用：7難度：0.6

  解析

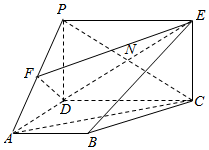• 22．如圖，PD垂直于梯形ABCD所在的平面，∠ADC=∠BAD=90°．F為PA中點，PD=

  2

  ，AB=AD=

  1

  2

  CD=1．四邊形PDCE為矩形，線段PC交DE于點N．
  （Ⅰ）求證：AC∥平面DEF；
  （Ⅱ）求二面角A-BC-P的大小；
  （Ⅲ）在線段EF上是否存在一點Q，使得BQ與平面BCP所成角的大小為

  π

  6

  ？若存在，求出Q點所在的位置；若不存在，請說明理由．
  組卷：220引用：3難度：0.3

  解析