2023-2024學年江蘇省泰州市興化市楚水實驗學校、興化一中等四校高三(上)第一次段考數學試卷
發布:2024/9/9 12:0:9
一、單項選擇題:本大題共8小題,每小題5分,共40分,在每小題給出的四個選項中,只有一項是符合題目要求的
-
1.已知集合A={x||x|<3},B={x|2-x>0},則A∩B=( )
A.(-3,2) B.(2,3) C.(0,3) D.(-∞,3) 組卷:65引用:4難度:0.9 -
2.已知扇形面積為
,半徑是1,則扇形的圓心角是( )3π8A. 3π16B. 3π8C. 3π4D. 3π2組卷:1467引用:35難度:0.9 -
3.已知
,則sin(θ-π6)=12=( )cos(θ+π3)A. -32B. -12C. 12D. 32組卷:218引用:7難度:0.8 -
4.已知函數
,滿足對任意x1≠x2,都有f(x)=ax,x<0(a-2)x+3a,x≥0成立,則a的取值范圍是( )f(x1)-f(x2)x1-x2<0A.(0,1) B. [34,1)C. (0,13]D. [34,2)組卷:653引用:13難度:0.6 -
5.已知a=eln3-ln2,b=2sin250°,c=log25,則a,b,c的大小關系為( )
A.a>b>c B.c>b>a C.c>a>b D.b>c>a 組卷:61引用:5難度:0.6 -
6.已知關于x的不等式x2-4ax+3a2<0(a<0)的解集為(x1,x2),則
的最大值是( )x1+x2+ax1x2A. 63B.- 233C. 433D. -433組卷:1252引用:35難度:0.9 -
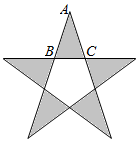 7.人們通常把頂角為36°的等腰三角形稱為黃金三角形,因為它的底邊和腰長的比值等于黃金分割比,我們熟悉的五角星就是由5個黃金三角形和1個正五邊形組成的,如圖,△ABC就是一個黃金三角形,根據以上信息,可得sin54°=( )5-12
7.人們通常把頂角為36°的等腰三角形稱為黃金三角形,因為它的底邊和腰長的比值等于黃金分割比,我們熟悉的五角星就是由5個黃金三角形和1個正五邊形組成的,如圖,△ABC就是一個黃金三角形,根據以上信息,可得sin54°=( )5-12A. 1+54B. 3+58C. 4+58D. 25-14組卷:63引用:5難度:0.6
四、解答題:共70分、解答應寫出文字說明,證明過程或演算步驟.
-
21.已知函數
的值域為[-1,3].f(x)=2asinax+acos(ax+π4)+b(a>0)
(1)求f(x)的單調遞增區間;
(2)若f(ωx)(ω>0)在上恰有一個零點,求ω的取值范圍.[0,π6]組卷:256引用:2難度:0.6 -
22.已知a∈R,函數
,x∈[0,2π].f(x)=sinxex+ax
(1)記f(x)的導函數為g(x),求g(x)在[0,2π]上的單調區間;
(2)若f(x)在(0,2π)上的極大值、極小值恰好各有一個,求a的取值范圍.組卷:51引用:3難度:0.6


