2021-2022學年山東省泰安六中八年級（下）期中數學試卷（五四學制）

一、選擇題（本大題共12個小題，每小題4分，共4分每小題給出的四個選項中，只有一項是符合題目要求的，請把正確答案的字母代號選出來填入下面答案欄的對應位置）

• 1．若式子

  x

  -

  1

  x

  -

  2

  在實數范圍內有意義，則x的取值范圍是（　　）

  A．x≥1且x≠2

  B．x≤1

  C．x＞1且x≠2

  D．x＜1
  組卷：3445引用：41難度：0.9

  解析

• 2．下列各式中，是最簡二次根式的是（　　）

  A． 8 x

  B． 5 x 3 y

  C． 16 a 2 + 25 b 2

  D． x 2
  組卷：14引用：1難度：0.8

  解析

• 3．下列運算正確的是（　　）

  A． 2 + 3 = 5

  B． 2 2 × 3 2 = 6 2

  C． 8 ÷ 2 = 2

  D． 3 2 - 2 = 3
  組卷：3000引用：80難度：0.9

  解析

• 4．關于x的一元二次方程（a-2）x²+x+a²-4=0的一個根為0，則a值為（　　）

  A．2

  B．-2

  C．±2

  D．0
  組卷：127引用：7難度：0.6

  解析

• 5．將一元二次方程x²+4x-5=0轉化成（x+a）²=b的形式，正確的是（　　）

  A．（x+2）2=9

  B．（x-2）2=9

  C．（x+2）2=1

  D．（x-2）2=1
  組卷：52引用：5難度：0.6

  解析

• 6．關于x的一元二次方程kx²+3x-1=0有實數根，則k的取值范圍是（　　）

  A．k≤- 9 4	B．k≥- 9 4 且k≠0
  C．k≥- 9 4	D．k＞- 9 4   且k≠0
  組卷：818引用：16難度：0.9

  解析

• 7．如圖，在長為100米，寬為80米的矩形場地上修建兩條寬度相等且互相垂直的道路，剩余部分進行綠化，要使綠化面積為7644米²，則道路的寬應為多少米？設道路的寬為x米，則可列方程為（　　）

  A．100×80-100x-80x=7644

  B．（100-x）（80-x）+x2=7644

  C．（100-x）（80-x）=7644

  D．100x+80x=356
  組卷：2083引用：120難度：0.9

  解析

• 8．已知菱形ABCD的對角線AC，BD的長度是關于x的方程x²-14x+48=0的兩個實數根，則此菱形的面積是（　　）

  A．20

  B．24

  C．48

  D．不確定
  組卷：458引用：7難度：0.7

  解析

• 9．如圖，四邊形ABCD中，對角線相交于點O，E、F、G、H分別是AD、BD、BC、AC的中點，要使四邊形EFGH是菱形，則四邊形ABCD需滿足的條件是（　　）

  A．AB=AD

  B．AC=BD

  C．AD=BC

  D．AB=CD
  組卷：3823引用：14難度：0.7

  解析

三、解答題（本大題共7道小題，滿分70分。解答題應寫出計算過程、文字說明或推演步驟）

• 26．如圖．在?ABCD中，E、F分別是邊AB、CD的中點，連接DE、BF、BD．
  （1）求證：DE∥BF；
  （2）過A點作AG∥DB交CB的延長線于點G．若∠G=90°，求證：四邊形DEBF是菱形．
  組卷：81引用：2難度：0.5

  解析

• 27．下面是一種類比、拓展的探究案例，先閱讀再解決后面的問題：
  已知正方形ABCD，點M在是直線BC上一個動點，點N在直線DC上，且滿足∠MAN=45°，連接MN．
  （1）如圖1，當點M在邊BC上時，求證：MN=BM+DN．
  請根據下面的思路分析填空：
  延長線段CD至點E，使得DE=BM，連接AE，根據正方形性質和作圖可證△ABM≌

  ，得到AM=AE，接著可證明△AMN≌

  ，可得出MN=

  ，再由線段的加法可以得出MN=BM+DN．
  （2）如圖2，當點M在邊CB的延長線上，點N在DC的延長線上；
  ①猜想BM，DN，MN之間有怎樣的數量關系？并證明你的猜想．
  ②若BC=4，BM=1，求CN．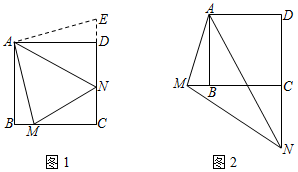
  
  組卷：217引用：3難度：0.2

  解析