2006年上海地區(qū)素質(zhì)競賽試卷
發(fā)布：2024/4/20 14:35:0
一、選擇題（共4小題，每小題4分，滿分16分）
-
1．下列運算正確的是（ ）
組卷：49引用：6難度：0.9 -
2．右邊給出的是2004年3月份的日歷表，任意圈出一豎列上相鄰的三個數(shù)，請你運用方程思想來研究，發(fā)現(xiàn)這三個數(shù)的和不可能是（ ）組卷：434引用：52難度：0.9 -
3．用10根等長的火柴棍首尾連接拼成一個三角形（火柴棍不允許剩余、重疊和折斷），這個三角形一定是（ ）
組卷：93引用：4難度：0.9 -
4．身高相等的三名同學(xué)甲，乙，丙參加風(fēng)箏比賽，三人放出風(fēng)箏的線長，線與地面夾角如下表（假設(shè)風(fēng)箏線是拉直的），則三人所放的風(fēng)箏中（ ）
同學(xué) 甲 乙 丙 放出風(fēng)箏線長 100m 100m 90m 線與地面交角 40° 45° 60° 組卷：202引用：16難度：0.7
三、解答題（共2小題，滿分20分）
-
11．推理能力都很強的甲、乙、丙站成一列，丙可以看見甲、乙，乙可以看見甲但看不見丙，甲看不見乙、丙．現(xiàn)有5頂帽子，3頂白色，2頂黑色．老師分別給每人戴上一頂帽子（在各自不知道的情況下）．老師先問丙是否知道頭上的帽子顏色，丙回答說不知道；老師再問乙是否知道頭上的帽子顏色，乙也回答說不知道；老師最后問甲是否知道頭上的帽子顏色，甲回答說知道．請你說出甲戴了什么顏色的帽子，并寫出推理過程．
組卷：605引用：4難度：0.5 -
12．如圖，正方形ABCD的邊長為4，點P是AB上不與A、B重合的任意一點，作PQ⊥DP，Q在BC上，設(shè)AP=x,BQ=y,
（1）求y與x之間的函數(shù)關(guān)系式，并指出自變量x的取值范圍；
（2）求函數(shù)圖象的頂點坐標(biāo)，并作出大致圖象．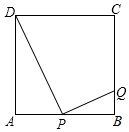
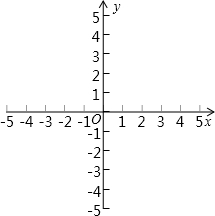組卷：141引用：1難度：0.1