2022-2023學年河南省豫南九校高三（上）第一次聯考數學試卷（文科）

一、選擇題（本大題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．若集合A={0，1，3，4，7}，B={-2，0，3，4}，則A∩B中元素的個數為（　　）

  A．2

  B．3

  C．4

  D．1
  組卷：12引用：3難度：0.7

  解析

• 2．已知復數z=（2+3i）（4i-7），其中i為虛數單位，則z的虛部為（　　）

  A．-26

  B．26

  C．-13

  D．13
  組卷：54引用：6難度：0.7

  解析

• 3．為了調查某工廠生產的一批口罩的質量情況，隨機抽取了1000個口罩，所得數據如圖所示，據此估計，這批口罩質量指標值的眾數（同一組中的數據用該組區間的中點值做代表）與中位數之和為（　　）
  

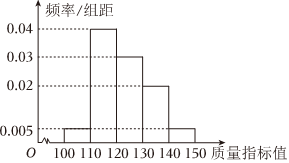
  A． 244 1 6

  B． 237 1 2

  C． 236 2 3

  D． 235 2 3
  組卷：91引用：3難度：0.8

  解析

• 4．已知等比數列{a_n}的前n項和為S_n，若a₄=81，a₁=3，則S₆=（　　）

  A．364

  B．1094

  C．368

  D．1092
  組卷：25引用：2難度：0.7

  解析

• 5．如圖所示，某拱橋的截面圖可以看作雙曲線

  y

  2

  16

  -

  x

  2

  m

  =

  1

  的圖象的一部分，當拱頂M到水面的距離為4米時，水面寬AB為

  4

  3

  米，則當水面寬度為

  4

  6

  米時，拱頂M到水面的距離為（　　）

  A．4米

  B．（8 2 -4）米

  C． （ 2 6 - 4 ） 米

  D． （ 4 7 - 4 ） 米
  組卷：37引用：5難度：0.7

  解析

• 6．如圖中小正方形的邊長為1，粗線畫出的是某幾何體的三視圖，則該幾何體的體積為（　　）

  A．4π

  B． （ 16 3 - 2 ） π

  C． 10 3 π

  D． （ 16 3 - 3 ） π
  組卷：26引用：2難度：0.7

  解析

• 7．執行如圖所示的程序框圖，若輸出的結果

  s

  =

  1

  +

  1

  3

  +

  1

  5

  +

  ?

  +

  1

  2023

  ，則判斷框中填入的條件可以為（　　）

  A．i≤2023

  B．i≤1013

  C．i≤1011

  D．i≤1012
  組卷：33引用：5難度：0.7

  解析

（二）選考題：10分．請考生在第22、23題中任選一題作答，如果多做，則按所做的第一題記分．作答時，請用2B鉛筆在答題卡上把所選題目對應的題號方框涂黑．[選修4-4：坐標系與參數方程]

• 22．已知平面直角坐標系xOy中，曲線C的參數方程為

  x = 8 sinα - 6 cosα

  y = 18 5 sinα + 24 5 cosα

  （其中α為參數）．以坐標原點為極點，x軸的非負半軸為極軸，建立極坐標系，直線l的極坐標方程為ρcos（{θ-

  π

  6

  ）=

  3

  ，點A的極坐標為（2，0）．
  （1）求曲線C的普通方程以及直線l的直角坐標方程；
  （2）若直線l與曲線C交于P，Q兩點，求|AP|?|AQ|的值．
  組卷：45引用：2難度：0.5

  解析

[選修4-5：不等式選講]

• 23．已知函數f（x）=|2x-3|+|3x+1|，且f（x）＜8的解集為{x|a＜x＜b}．
  （1）求a,b的值；
  （2）若正數m,n,p滿足3^m+n+p=9，求證：

  n

  2

  +

  p

  2

  m

  +

  m

  2

  +

  p

  2

  n

  +

  m

  2

  +

  n

  2

  p

  ≥2b.
  組卷：6引用：2難度：0.5

  解析