2020-2021學年江蘇省南京二十九中高二（下）周練數學試卷（009）

一、單項選擇題：（每題5分，共40分）

• 1．設a∈Z，且0≤a＜13，若51²⁰¹⁸+a能被13整除，則a的值為（　　）

  A．0

  B．1

  C．11

  D．12
  組卷：43引用：2難度：0.6

  解析

• 2．函數y=xcosx+sinx在區間[-π，π]上的圖象可能是（　　）

  A．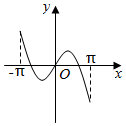

  B．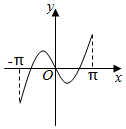

  C．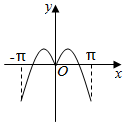

  D．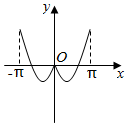
  組卷：4513引用：43難度：0.7

  解析

• 3．已知向量

  a

  =（-1，3），

  b

  =

  （

  λ

  ，

  3

  3

  ）

  ，若

  a

  ⊥

  b

  ，則

  a

  +

  3

  b

  與

  a

  的夾角為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  組卷：489引用：3難度：0.7

  解析

• 4．若把單詞“error”的字母順序寫錯了，則可能出現的錯誤寫法的種數為（　　）

  A．17

  B．18

  C．19

  D．20
  組卷：374引用：5難度：0.6

  解析

• 5．（x+

  y

  2

  x

  ）（x+y）⁵的展開式中x³y³的系數為（　　）

  A．5

  B．10

  C．15

  D．20
  組卷：7241引用：16難度：0.7

  解析

• 6．已知函數f（x）=

  2

  sinωx和g（x）=

  2

  cosωx（ω＞0）圖象的交點中，任意連續三個交點均可作為一個等腰直角三角形的頂點，為了得到y=g（x）的圖象，只需把y=f（x）的圖象（　　）

  A．向左平移1個單位	B．向左平移 π 2 個單位
  C．向右平移1個單位	D．向右平移 π 2 個單位
  組卷：499引用：5難度：0.5

  解析

• 7．小趙、小錢、小孫、小李到4個景點旅游，每人只去一個景點，設事件A為“4個人去的景點不完全相同”，事件B為“小趙獨自去一個景點”，則P（B|A）=（　　）

  A． 3 7

  B． 4 7

  C． 5 7

  D． 6 7
  組卷：680引用：4難度：0.7

  解析

四、解答題：本大題共6小題，請在答題卡指定的區城內作答，解答時應寫出文字說明、證明過程或演算步驟.

• 21．為了嚴格監控某種零件的一條生產線的生產過程，某企業每天從該生產線上隨機抽取10000個零件，并測量其內徑（單位：cm）．根據長期生產經驗，認為這條生產線正常狀態下生產的零件的內徑X服從正態分布N（μ，σ²）．如果加工的零件內徑小于μ-3σ或大于μ+3σ均為不合格品，其余為合格品．
  （1）假設生產狀態正常，請估計一天內抽取的10000個零件中不合格品的個數約為多少；
  （2）若生產的某件產品為合格品則該件產品盈利；若生產的某件產品為不合格品則該件產品虧損．已知每件產品的利潤L（單位：元）與零件的內徑X有如下關系：

  L

  =

  - 5 ， X ＜ μ - 3 σ ，

  4 ， μ - 3 σ ≤ X ≤ μ - σ ，

  6 ， μ - σ ≤ X ≤ μ + 3 σ ，

  - 5 ， X ＞ μ + 3 σ .

  求該企業一天從生產線上隨機抽取10000個零件的平均利潤．
  附：若隨機變量X服從正態分布N（μ，σ²），有P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜X≤μ+3σ）=0.9974．
  組卷：283引用：2難度：0.7

  解析

• 22．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的左、右焦點分別為F₁，F₂，以F₂為圓心過橢圓左頂點M的圓與直線3x-4y+12=0相切于N，且滿足

  M

  F

  1

  =

  1

  2

  F

  1

  F

  2

  ．
  （1）求橢圓C的標準方程；
  （2）過橢圓C右焦點F₂的直線l與橢圓C交于不同的兩點A，B，問△F₁AB內切圓面積是否有最大值？若有，求出最大值；若沒有，說明理由．
  組卷：135引用：3難度：0.5

  解析