2022-2023學年吉林市普通中學高二（上）期中數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一個符合題目要求。

• 1．已知

  a

  =（-2，1，2），

  b

  =（-1，t,1），若

  a

  ⊥

  b

  ，則實數t的值為（　　）

  A．0

  B．-4

  C． 1 2

  D．4
  組卷：83引用：4難度：0.8

  解析

• 2．經過點M（1，-1）且與直線x+4y+2=0垂直的直線方程為（　　）

  A．x+4y+3=0

  B．x-4y+5=0

  C．4x-y-5=0

  D．4x+y-3=0
  組卷：66引用：4難度：0.7

  解析

• 3．直線（m²+1）x-y+1=0的傾斜角的取值范圍是（　　）

  A．[0， π 4 ）	B．[0， π 2 ）
  C．[ π 4 ， π 2 ）∪（ π 2 ，π）	D．[ π 4 ， π 2 ）
  組卷：70引用：3難度：0.7

  解析

• 4．過點（1，

  3

  2

  ）且與橢圓

  x

  2

  2

  +

  y

  2

  =1有相同焦點的橢圓方程為（　　）

  A． x 2 5 + y 2 4 =1

  B． x 2 4 + y 2 3 =1

  C． x 2 4 + y 2 5 =1

  D． x 2 3 + y 2 4 =1
  組卷：130引用：3難度：0.7

  解析

• 5．直線x+my+m=0與圓（x-1）²+（y-1）²=9的位置關系為（　　）

  A．相交	B．相切
  C．相離	D．與m的值有關
  組卷：142引用：6難度：0.6

  解析

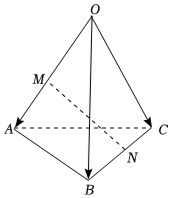• 6．如圖，在四面體OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，點M在OA上，點N在BC上，且OM=2MA，BN=2NC，則

  MN

  =（　　）

  A．- 2 3 a + 1 3 b + 2 3 c	B． 2 3 a - 2 3 b + 1 3 c
  C．- 2 3 a - 1 3 b + 2 3 c	D． 2 3 a - 2 3 b - 1 3 c
  組卷：76引用：5難度：0.8

  解析

• 7．已知圓C₁：x²+y²=4與x軸交于A，B兩點，圓C₂：（x-3）²+（y-4）²=a,若圓C₂上存在點P使得∠APB=90°，則a的取值范圍是（　　）

  A．[7，+∞）

  B．[9，+∞）

  C．[9，49]

  D．[3，7]
  組卷：91引用：3難度：0.7

  解析

四、解答題：本大題共6小題，共70分。解答應寫出文字說明，證明過程或演算步驟。

• 21．如圖，直三棱柱ABC-A₁B₁C₁中，AA₁=AB=BC=2，BC⊥AB，M為棱A₁C₁的中點，P為棱BB₁上一動點．
  （Ⅰ）試確定點P位置，使得MP∥平面A₁BC；
  （Ⅱ）求點C₁到平面A₁PC距離的最大值．
  組卷：44引用：7難度：0.7

  解析

• 22．已知，橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  6

  3

  ，長軸長為2

  3

  ．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）直線l過點（2，0），且被橢圓C截得的弦長為

  2

  6

  3

  ，求直線l的方程；
  （Ⅲ）設O為坐標原點，若P，Q，M為橢圓上的點，且圓M與直線OP，OQ相切，當直線OP，OQ的斜率存在且k_OP．k_OQ=-

  1

  3

  ，求圓M的半徑．
  組卷：77引用：3難度：0.3

  解析