2022-2023學年江西省宜春市豐城中學七年級（下）期末數學試卷

一．選擇題（共6小題，18分）

• 1．以下調查中，適合全面調查的是（　　）

  A．了解全國中學生的視力情況

  B．檢測“神舟十六號”飛船的零部件

  C．檢測臺州的城市空氣質量

  D．調查某池塘中現有魚的數量
  組卷：1052引用：14難度：0.8

  解析

• 2．如圖，AE∥CD，AC平分∠BCD，∠2=35°，∠D=60°，則∠B=（　　）

  A．52°

  B．50°

  C．45°

  D．25°
  組卷：599引用：15難度：0.7

  解析

• 3．如圖，正六邊形ABCDEF和正五邊形GHCDL的邊CD重合，DH的延長線與AB交于點P，則∠BPD的度數是（　　）

  A．83°

  B．84°

  C．85°

  D．86°
  組卷：343引用：4難度：0.8

  解析

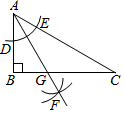• 4．如圖，在Rt△ABC中，∠B=90°，以點A為圓心，適當長為半徑畫弧，分別交AB、AC于點D，E，再分別以點D、E為圓心，大于

  1

  2

  DE為半徑畫弧，兩弧交于點F，作射線AF交邊BC于點G，若BG=1，AC=4，則△ACG的面積是（　　）

  A．1

  B． 3 2

  C．2

  D． 5 2
  組卷：1797引用：43難度：0.8

  解析

• 5．如圖，△ABC和△ADE均是等腰直角三角形，其中斜邊AD的端點D在斜邊BC的延長線上，AD，CE相交于點F，則以下判斷正確的是（　　）

  A．△ACE是等邊三角形	B．∠ADB=2∠CAD
  C．△CDE是等腰三角形	D．AF=2DF
  組卷：68引用：5難度：0.5

  解析

• 6．在△ABC中，∠ACB=90°，∠ABC=30°，△CDE是等邊三角形，點D在AB邊上，點E在△ABC外部，EH⊥AB于點H，過點E作GE∥AB，交線段AC的延長線于點G，AG=5CG，BH=3．則CG的長為（　　）

  A．1

  B．2

  C． 2

  D． 3
  組卷：785引用：5難度：0.3

  解析

二．填空題（共6小題，18分）

• 7．已知關于x,y的二元一次方程組

  ax + by = 6

  bx + ay = 8

  的解為

  x = 1

  y = 3

  ，若m,n滿足二元一次方程組

  a （ m + n ） + b （ m - n ） = 6

  b （ m + n ） + a （ m - n ） = 8

  ，則2m+3n的立方根是

  ．
  組卷：307引用：5難度：0.5

  解析

三．解答題（共11小題，13-17，每小題6分，18-20，每小題6分，21-22題，每題9分，23題12分）

• 22．如圖，在平面直角坐標系中，已知A（a,0）、B（0，b）分別在坐標軸的正半軸上．
  （1）如圖1，若a、b滿足（a-4）²+

  b

  -

  3

  =0，以B為直角頂點，AB為直角邊在第一象限內作等腰直角△ABC，則點C的坐標是

  ；
  （2）如圖2，若a=b,點D是OA的延長線上一點，以D為直角頂點，BD為直角邊在第一象限作等腰直角△BDE，連接AE，求證：∠ABD=∠AED；
  （3）如圖3，設AB=c,∠ABO的平分線過點D（2，-2），直接寫出a-b+c的值．
  
  組卷：1898引用：8難度：0.2

  解析

• 23．【初步探索】
  （1）如圖1：在四邊形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分別是BC、CD上的點，且EF=BE+FD，探究圖中∠BAE、∠FAD、∠EAF之間的數量關系．
  小王同學探究此問題的方法是：延長FD到點G，使DG=BE．連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結論，他的結論應是

  ；
  【靈活運用】
  （2）如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°．E、F分別是BC、CD上的點，且EF=BE+FD，上述結論是否仍然成立，并說明理由；
  【拓展延伸】
  （3）如圖3，已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=AD，若點E在CB的延長線上，點F在CD的延長線上，如圖3所示，仍然滿足EF=BE+FD，請寫出∠EAF與∠DAB的數量關系，并給出證明過程．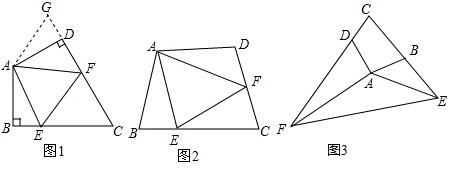
  
  組卷：4517引用：52難度：0.1

  解析