2021-2022學年福建省寧德市高一（下）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一個選項是符合題目要求的.

• 1．已知復數z=1-2i,則z的共軛復數

  z

  對應的點位于復平面的（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：38引用：5難度：0.9

  解析

• 2．已知四棱錐P-ABCD的所有棱長均相等，點E，F分別為線段PC，PD的中點，則異面直線EF與PB所成角的大小為（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：36引用：2難度：0.6

  解析

• 3．在△ABC中，D為BC上一點，且BD=2DC，則

  AD

  =（　　）

  A． AB + 1 3 AC

  B． AB - 1 3 AC

  C． 2 3 AB + 1 3 AC

  D． 1 3 AB + 2 3 AC
  組卷：551引用：11難度：0.8

  解析

• 4．若x₁，x₂，?，x₂₀₂₂的平均數為2，方差為1，且y_i=2x_i-1，i=1，2，?，2022，則y₁，y₂，?，y₂₀₂₂的平均數和方差分別為（　　）

  A．3，2

  B．3，3

  C．3，4

  D．4，4
  組卷：114引用：2難度：0.8

  解析

• 5．在一個實驗中，某種豚鼠被感染A病毒的概率均為40%，現采用隨機模擬方法估計三只豚鼠中被感染的概率：先由計算機產生出[0，9]之間整數值的隨機數，指定1，2，3，4表示被感染，5，6，7，8，9，0表示沒有被感染．經隨機模擬產生了如下20組隨機數：
  192   907   966   925   271   932   812   458   569   683
  257   393   127   556   488   730   113   537   989   431
  據此估計三只豚鼠中至少一只被感染的概率為（　　）

  A．0.25

  B．0.4

  C．0.6

  D．0.75
  組卷：148引用：10難度：0.6

  解析

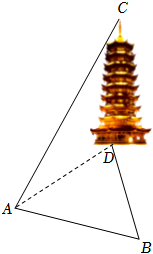• 6．某校研究性學習小組想要測量某塔的高度，現選取與塔底D在同一個水平面內的兩個測量基點A與B，現測得∠DAB=75°，∠ABD=60°，AB=48米，在點A處測得塔頂C的仰角為30°，則塔高CD為（　　）米．

  A． 24 2

  B． 24 3

  C． 24 6

  D． 32 2
  組卷：88引用：5難度：0.7

  解析

• 7．已知直線m、n和平面α、β，下列命題正確的是（　　）

  A．若m∥n,n?α，則m∥α

  B．若m∥α，n∥α，m、n?β，則α∥β

  C．若α⊥β，m?α，則m⊥β

  D．若m⊥α，α⊥β，則m∥β或m?β
  組卷：161引用：2難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

• 21．羽毛球比賽規則：
  ①21分制，每球取勝加1分，由勝球方發球；
  ②當雙方比分為20：20之后，領先對方2分的一方贏得該局比賽；
  當雙方比分為29：29時，先取得30分的一方贏得該局比賽．經過鏖戰，甲乙比分為27：28，甲在關鍵時刻贏了一球，比分變為28：28．在最后關頭，按以往戰績統計，甲發球時，甲贏球的概率為0.4，乙發球時，甲贏球的概率為0.5，每球勝負相互獨立．
  （1）甲乙雙方比分為28：28之后，求再打完兩球該局比賽結束的概率；
  （2）甲乙雙方比分為28：28之后，求甲贏得該局比賽的概率．
  組卷：95引用：3難度：0.6

  解析

• 22．如圖，已知等腰梯形ABCD的外接圓半徑為2，AB∥CD，AB=2CD，點P是上半圓上的動點（不包含A，B兩點），點Q是線段PA上的動點，將半圓APB所在的平面沿直徑AB折起使得平面PAB⊥平面ABCD．
  
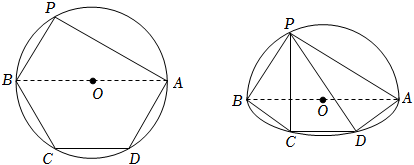
  （1）求三棱錐P-ACD體積的最大值；
  （2）當PC∥平面QBD時，求

  |

  PQ

  |

  |

  QA

  |

  的值；
  （3）設QB與平面ABD所成的角為α，二面角Q-BD-A的平面角為β．求證：tanβ=2tanα．
  組卷：105引用：4難度：0.5

  解析