當前位置：試卷中心 > 試卷詳情

2013-2014學年浙江省金華一中高三（下）周測數學試卷（6）

發布：2024/4/20 14:35:0

一、選擇題：本大題共12小題，每小題5分，在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知集合A={x|-5≤2x-1≤3，x∈R}，B={x|x（x-8）≤0，x∈Z}，則A∩B=（　　）
A．（0，2） B．[0，2] C．{0，2} D．{0，1，2}
組卷：43引用：19難度：0.9
解析
2．如果復數
m
2
+
i
1
-
mi
是實數，則實數m=（　　）
A．-1 B．1 C．
-
2
D．
2
組卷：12引用：9難度：0.9
解析
3．焦點為（0，6），且與雙曲線
x
2
2
-
y
2
=1有相同的漸近線的雙曲線方程是（　　）
A．
x
2
12
-
y
2
24
=
1
B．
y
2
12
-
x
2
24
=
1
C．
y
2
24
-
x
2
12
=
1
D．
x
2
24
-
y
2
12
=
1
組卷：703引用：51難度：0.9
解析
4．在△ABC中，角A，B，C所對的邊分別為a,b,c,若a=
2
，b=2，sinB+cosB=
2
，則角A的大小為（　　）
A．60° B．30° C．150° D．45°
組卷：183引用：12難度：0.9
解析
5．已知數列{a_n}是各項均為正數且公比不等于1的等比數列．對于函數y=f（x），若數列{lnf（a_n）}為等差數列，則稱函數f（x）為“保比差數列函數”．現有定義在（0，+∞）上的如下函數：
①
f
（
x
）
=
1
x
，
②f（x）=x²，
③f（x）=e^x，
④
f
（
x
）
=
x
，
則為“保比差數列函數”的所有序號為（　　）
A．①② B．③④ C．①②④ D．②③④
組卷：114引用：15難度：0.7
解析
6．利用如圖所示程序框圖在直角坐標平面上打印一系列點，則打印的點落在坐標軸上的個數是（　　）
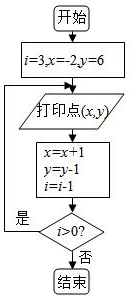
A．0 B．1 C．2 D．3
組卷：484引用：24難度：0.9
解析
7．在△ABC中，
AB
+
AC
=2
AM
，|
AM
|=1，點P在AM上且滿足
AP
=2
PM
，則
PA
?（
PB
+
PC
）等于（　　）
A．
4
9
B．
4
3
C．-
4
3
D．-
4
9
組卷：952引用：11難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題：（解答應寫出文字說明，證明過程或演算步驟．）

20．在平面直角坐標系中，已知點
A
（
1
2
，
0
）
，向量
e
=
（
0
，
1
）
，點B為直線
x
=
-
1
2
上的動點，點C滿足
2
OC
=
OA
+
OB
，點M滿足
BM
?
e
=
0
，
CM
?
AB
=
0
．
（1）試求動點M的軌跡E的方程；
（2）設點P是軌跡E上的動點，點R、N在y軸上，圓（x-1）²+y²=1內切于△PRN，求△PRN的面積的最小值．
組卷：52引用：6難度：0.5
解析
21．已知函數f（x）=ax²+lnx（a∈R）．
（1）當a=
1
2
時，求f（x）在區間[1，e]上的最大值和最小值；
（2）如果函數g（x），f₁（x），f₂（x），在公共定義域D上，滿足f₁（x）＜g（x）＜f₂（x），那么就稱g（x）為f₁（x），f₂（x）的“活動函數“．已知函數
f
1
（
x
）
=
（
a
-
1
2
）
x
2
+
2
ax
+
（
1
-
a
2
）
lnx
，f₂（x）=
1
2
x
2
+2ax.若在區間（1，+∞）上函數f（x）是f₁（x），f₂（x）的“活動函數“，求a的取值范圍
組卷：1089引用：25難度：0.1
解析