2022-2023學年浙江省紹興市紹初教育集團九年級（上）期中數學試卷

一、選擇題（共10小題，每小題4分，共40分）

• 1．下列成語或詞語所反映的事件中，可能性最小的是（　　）

  A．瓜熟蒂落

  B．旭日東升

  C．守株待兔

  D．夕陽西下
  組卷：922引用：15難度：0.6

  解析

• 2．已知二次函數y=x²-2x+4，下列結論不正確的是（　　）

  A．開口向上

  B．有最大值3

  C．當x≥1時，y隨x的增大而增大

  D．關于直線x=1對稱
  組卷：71引用：2難度：0.6

  解析

• 3．如圖，四邊形ABCD內接于⊙O，連接OB，OD，若∠BOD=110°，則∠BCD的度數（　　）

  A．55°

  B．70°

  C．110°

  D．125°
  組卷：89引用：2難度：0.7

  解析

• 4．一個袋子中裝有12個球（袋中每個球除顏色外其余都相同）．其活動小組想估計袋子中紅球的個數，分10個組進行摸球試驗，每一組做400次試驗，匯總后，摸到紅球的次數為3000次．請你估計袋中紅球接近（　　）

  A．3

  B．4

  C．6

  D．9
  組卷：260引用：5難度：0.6

  解析

• 5．如圖，已知二次函數y=-x²+2x,當-1＜x＜a時，y隨x的增大而增大，則實數a的取值范圍是（　　）

  A．a＞1

  B．-1＜a≤1

  C．-1＜a＜1

  D．-1＜a＜2
  組卷：240引用：3難度：0.6

  解析

• 6．已知拋物線y=x²+mx的對稱軸為直線x=2，則關于x的方程x²+mx=5的根是（　　）

  A．0，4

  B．1，5

  C．1，-5

  D．-1，5
  組卷：2666引用：12難度：0.6

  解析

• 7．如圖，已知BC是⊙O的直徑，半徑OA⊥BC，點D在劣弧AC上（不與點A，點C重合），BD與OA交于點E，設∠AED=α，∠AOD=β，則以下關系式成立的是（　　）

  A．2α+β=180°

  B．2α-β=90°

  C．3α+β=180°

  D．3α-β=90°
  組卷：1014引用：5難度：0.5

  解析

• 8．如圖，⊙O是等邊△ABC的外接圓，點D是弧AC上一動點（不與A，C重合），下列結論：①∠ADB=∠BDC；②DA=DC；③當DB最長時，DB=2DC；④DA+DC=DB，其中一定正確的結論有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：3363引用：14難度：0.5

  解析

三、解答題（共8小題，第17-20題每小題8分，第21題10分，第22、23題每小題8分，第24題14分，共80分）

• 23．定義：對角線互相垂直的圓內接四邊形稱為圓的神奇四邊形．
  （1）如圖1，已知四邊形ABCD是⊙O的神奇四邊形，若AC=12，BD=10，則S_{四邊形ABCD}=

  ；
  （2）如圖2，已知四邊形ABCD為⊙O的內接四邊形，連接OA，OB，OC，OD，滿足∠BOC+∠AOD=180°，求證：四邊形ABCD是⊙O的神奇四邊形；
  （3）如圖3，已知四邊形ABCD是⊙O的神奇四邊形，∠BAD=90°，延長AD，BC相交于點E，若AB=6，AE=8，求AC的長．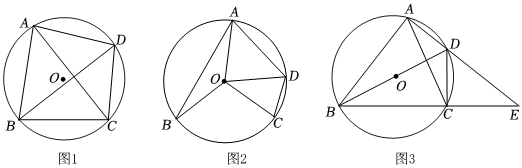
  
  組卷：213引用：1難度：0.6

  解析

• 24．如圖1，在平面直角坐標系xOy中，直線y=kx+3分別交x軸，y軸于A，B兩點，經過A，B兩點的拋物線y=-x²+bx+c與x軸的負半軸相交于點C（-1，0）．
  （1）求拋物線的解析式和直線BC的解析式；
  （2）如圖2，點P為線段AB上的點，且點P的橫坐標為m,過P作y軸的平行線交拋物線于M，連接BM．
  ①當△PBM是MP為腰的等腰三角形時，求MP的長；
  ②若拋物線頂點D在以PM、PB為鄰邊的平行四邊形的形內（不含邊界），求m的取值范圍．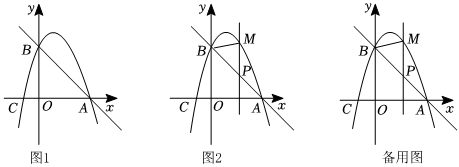
  
  組卷：200引用：1難度：0.2

  解析